Mathematics
In rhombus ABCD, the co-ordinates of point A and C are (2, -6) and (-4, 8) respectively. Find the equation of the diagonal BD.
Straight Line Eq
2 Likes
Answer
In a rhombus,
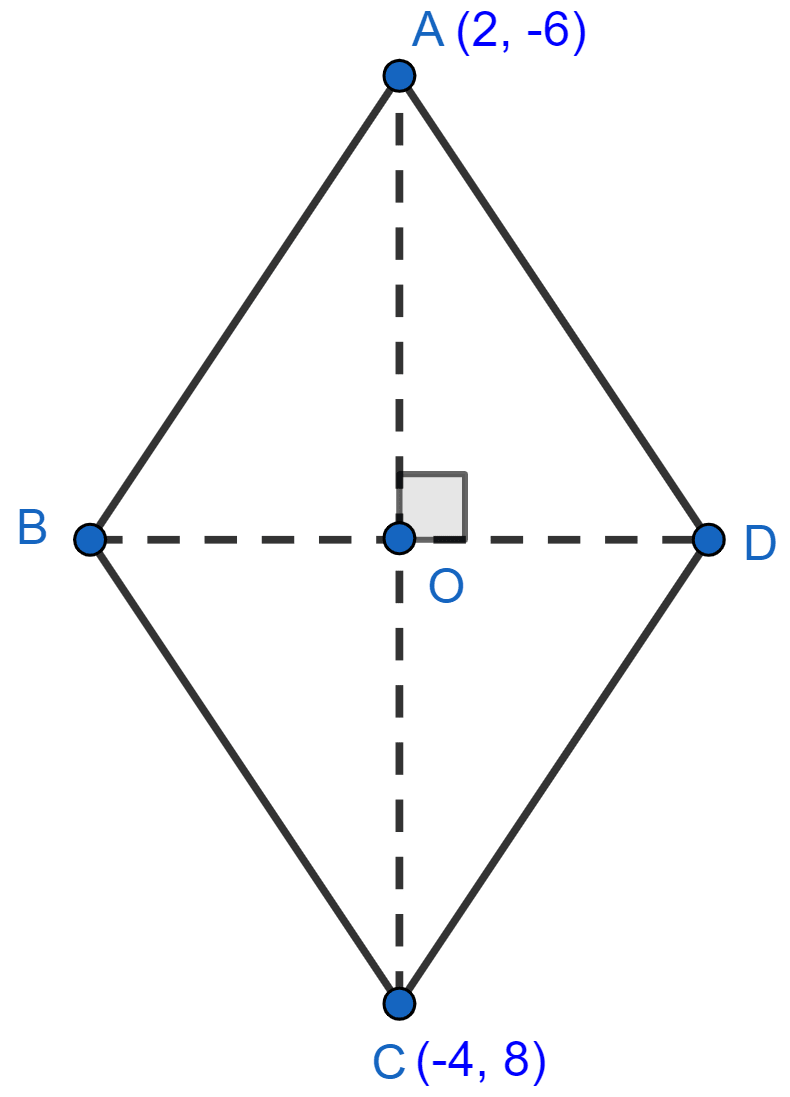
Diagonals bisect each other and are perpendicular.
So, mid-point of AC = mid-point of BD.
By formula,
Mid-point =
Let O be the point of intersection of diagonal AC and BD.
Substituting values we get :
= \Big(\dfrac{-2}{2}, \dfrac{2}{2}\Big) \\[1em]
= (-1, 1).
By formula,
Slope of line =
Substituting values we get :
Slope of AC = .
We know that,
Product of slope of perpendicular lines = -1.
⇒ Slope of AC × Slope of BD = -1
⇒ Slope of BD = -1
⇒ Slope of BD = .
By point-slope form,
Equation of line :
y - y1 = m(x - x1)
BD also passes through point O.
So,
Equation of line BD is
Hence, equation of line BD is 7y - 3x = 10.
Answered By
1 Like
Related Questions
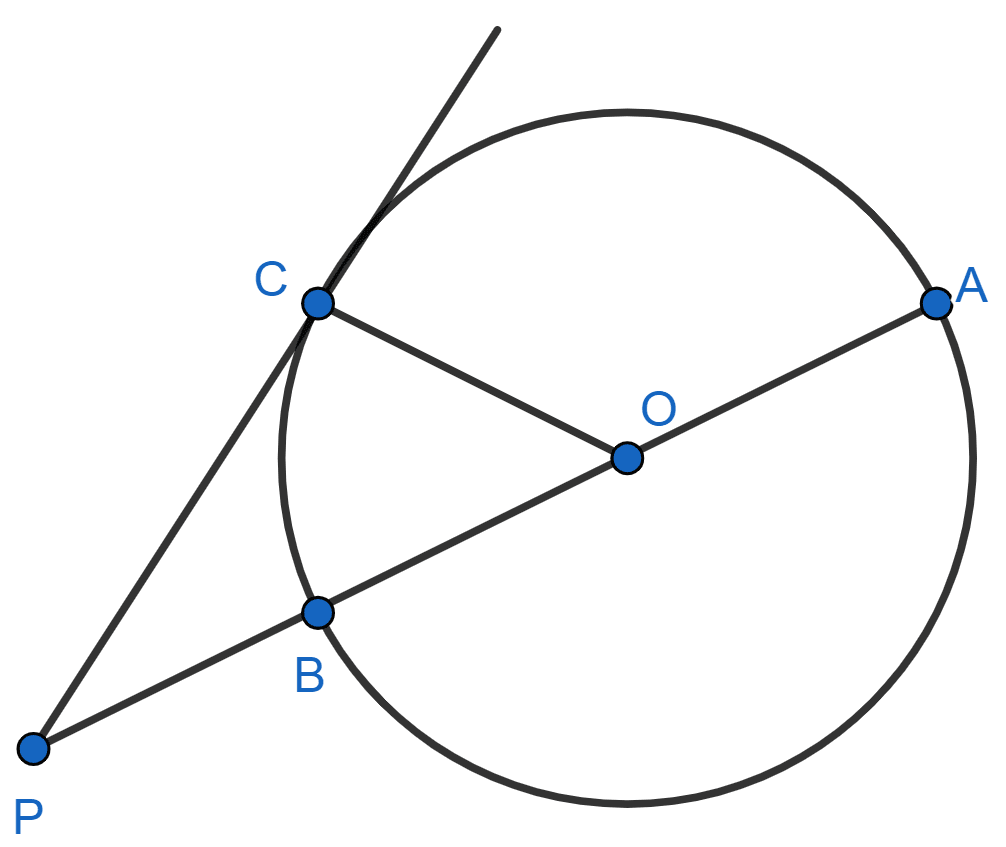
In the given figure, AB is diameter and PC is tangent to the circle with center O. If AP = 40 cm, CP = 20 cm, find the radius of the circle.
Prove that :
= 2 cosec A.
For what value of n, the nth term of A.P. 63, 65, 67, ….. and nth term of A.P. 3, 10, 17, …… are equal ?
Using remainder theorem, factorise 6x3 - 11x2 - 3x + 2 completely.