Mathematics
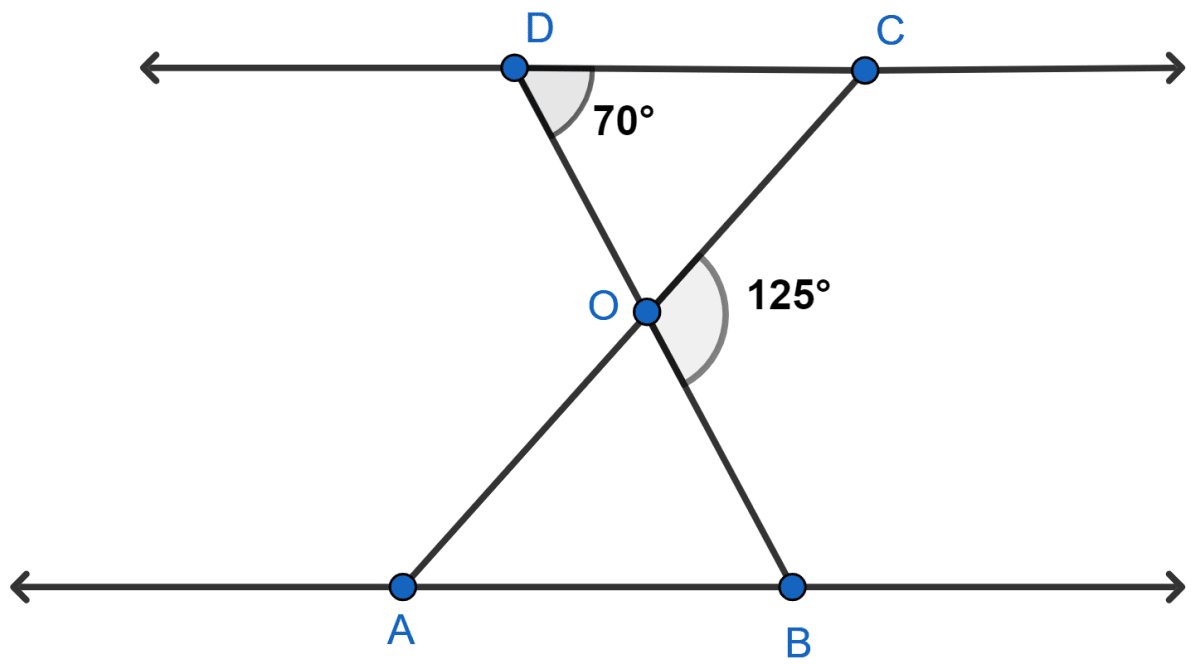
In given figure, △ ODC ~ △ OBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
Answer
From figure,
DOB is a straight line. So, ∠DOC and ∠BOC forms a linear pair.
⇒ ∠DOC + ∠BOC = 180°
⇒ ∠DOC + 125° = 180°
⇒ ∠DOC = 180° - 125° = 55°.
In △DOC,
⇒ ∠DOC + ∠CDO + ∠DCO = 180° [By angle sum property of triangle]
⇒ 55° + 70° + ∠DCO = 180°
⇒ ∠DCO = 180° - 125° = 55°.
From figure,
⇒ ∠OAB = ∠DCO = 55°. [Alternate angles are equal]
Hence, ∠DOC = 55°, ∠DCO = 55°, ∠OAB = 55°.
Related Questions
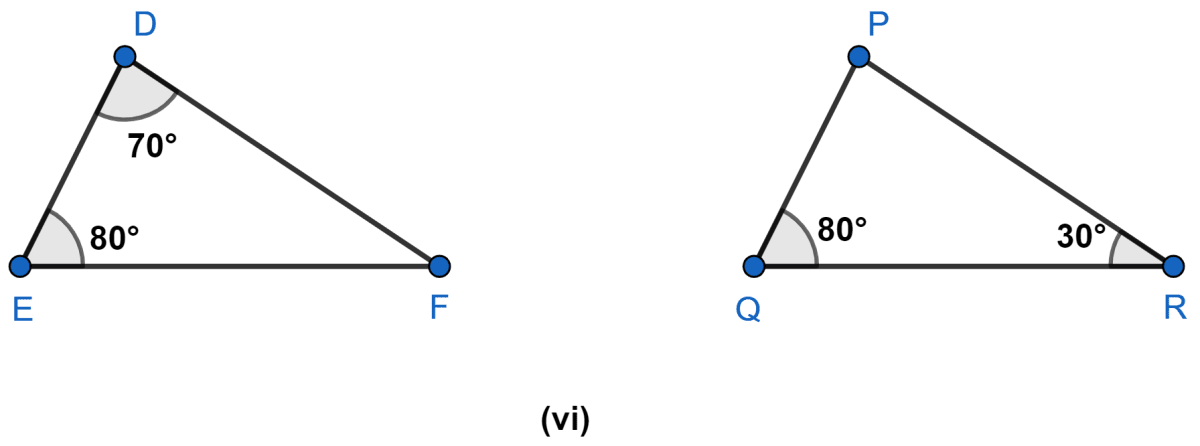
State which pairs of triangles are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :
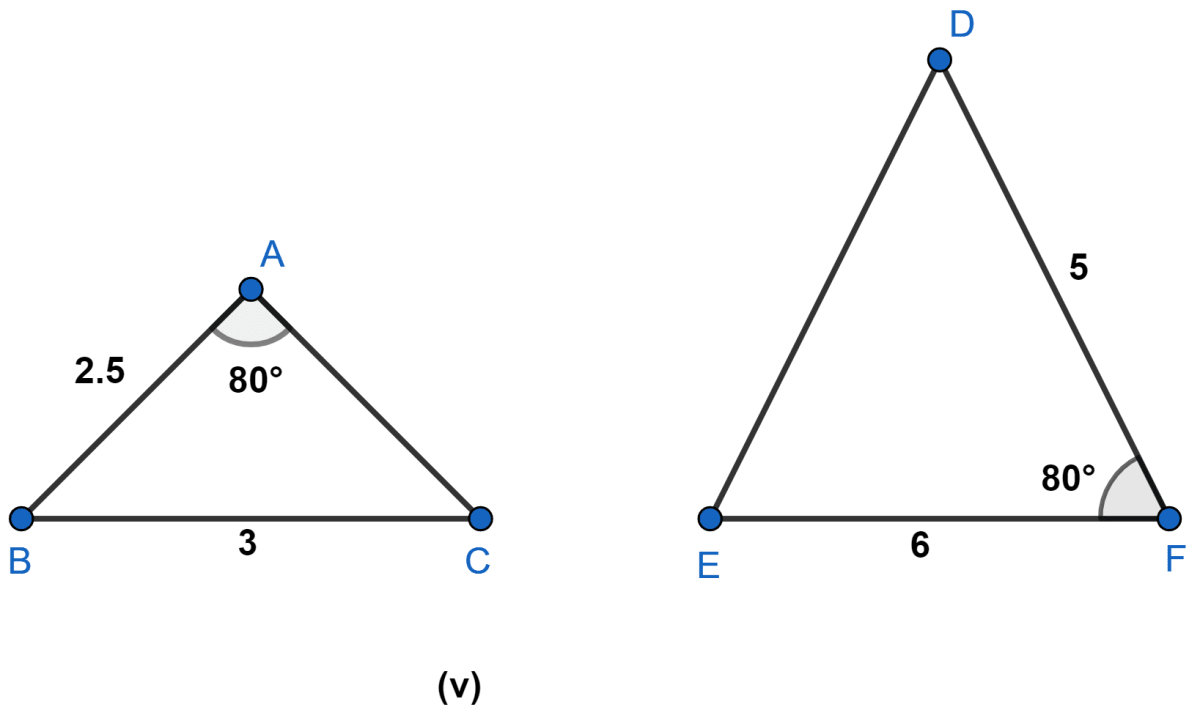
State which pairs of triangles are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :