Mathematics
In an equilateral triangle, prove that the centroid and the circumcentre of the triangle coincide.
Circles
85 Likes
Answer
From figure,
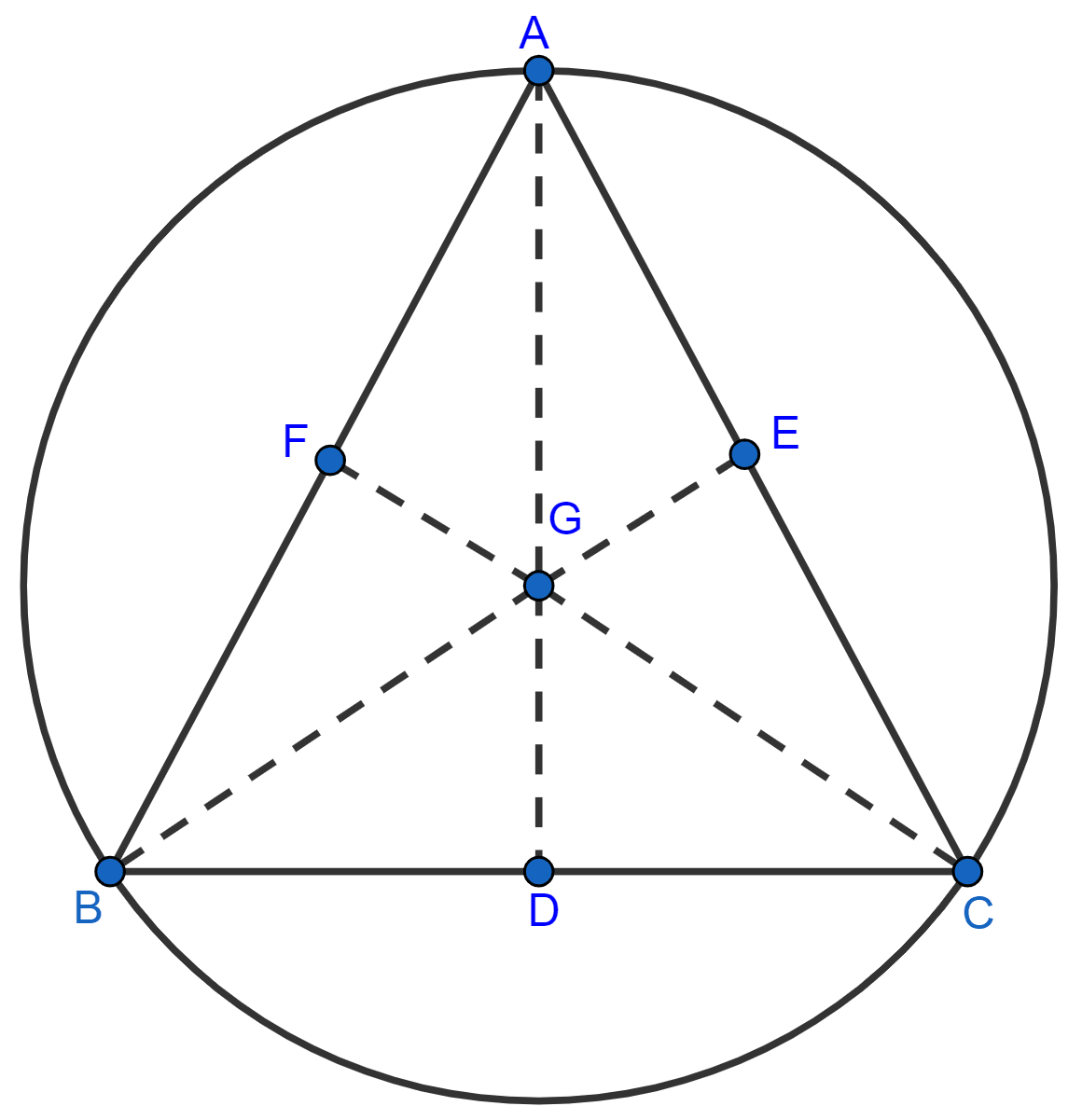
AD, BE and CF are medians of the triangle.
Let G be the centroid of triangle ABC.
Triangle ABC is an equilateral triangle,
∴ AB = BC = CA and ∠ABC = ∠BAC = ∠BCA = 60°
In △BFC and △BEC,
⇒ BC = BC (Common Side)
⇒ ∠FBC = ∠ECB = 60°.
⇒ BF = EC (As F is mid-point of AB and E is mid-point of AC and AB = AC.)
△BFC ≅ △BEC (By SAS axiom.)
∴ BE = CF (By C.P.C.T.) ………(1)
Now, in △ABE and △ABD
AB = AB (Common Side)
∠BAE = ∠ABD = 60°
BD = AE (As D is mid-point of BC and E is mid-point of AC and BC = AC.)
△ABE ≅ △ABD (By SAS axiom.)
∴ BE = AD (By C.P.C.T.) …………. (2)
From equation 1 and 2, we get:
⇒ AD = BE = CF
⇒
We know that G (the centroid) of the triangle divides the median in a 2 : 1 ratio.
∴ GA = GB = GC.
So, we can say that G is equidistant from the three vertices A. B and C.
G is circumcentre of ΔABC.
Hence, proved that the centroid and circumcentre are coincident.
Answered By
49 Likes
Related Questions
The line joining mid-points of two chords of a circle passes through its center. Prove that the chords are parallel.
If a diameter of a circle is perpendicular to one of two parallel chords of the circle, prove that it is perpendicular to the other and bisects it.
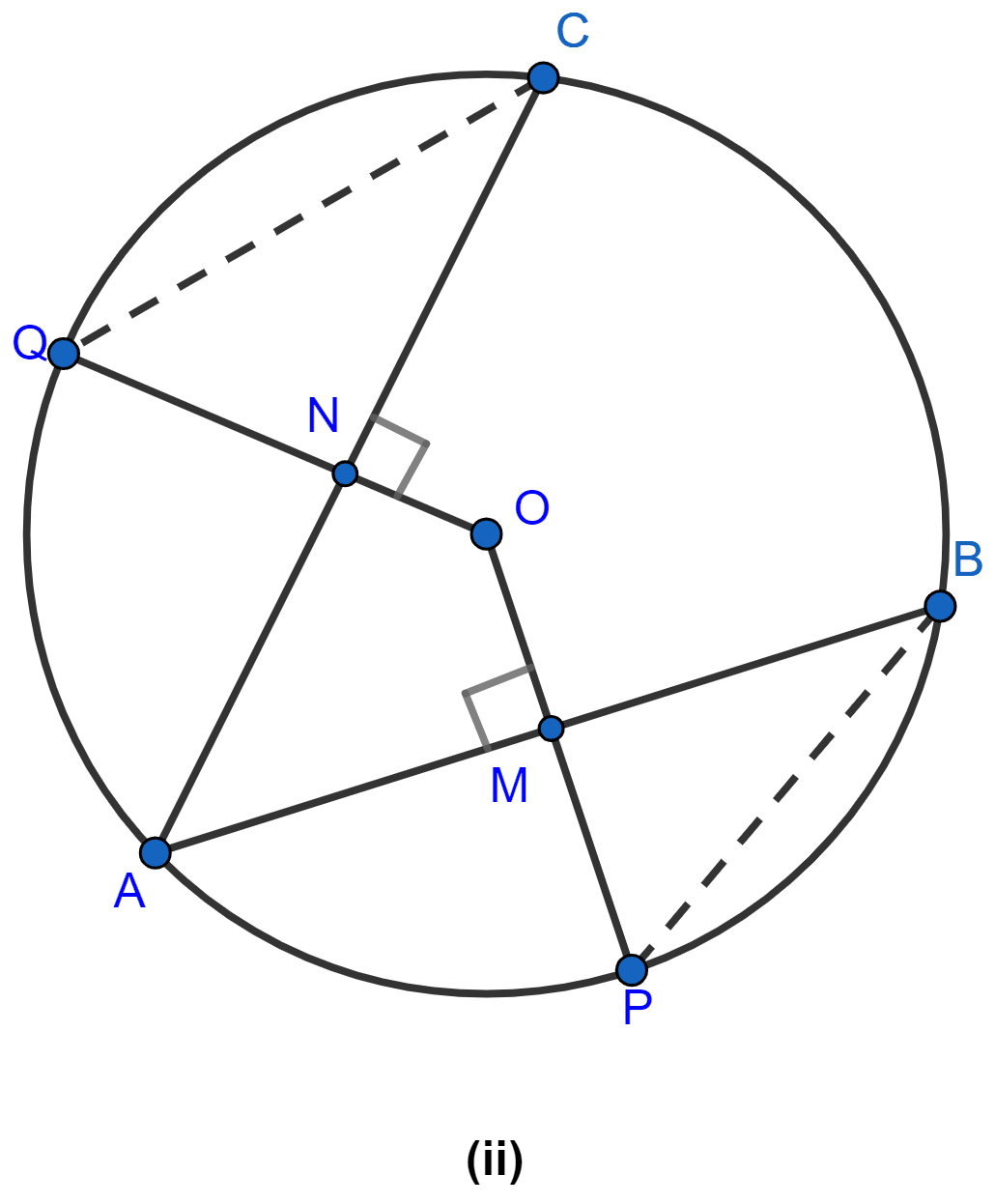
In the figure (i) given below, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2OD.
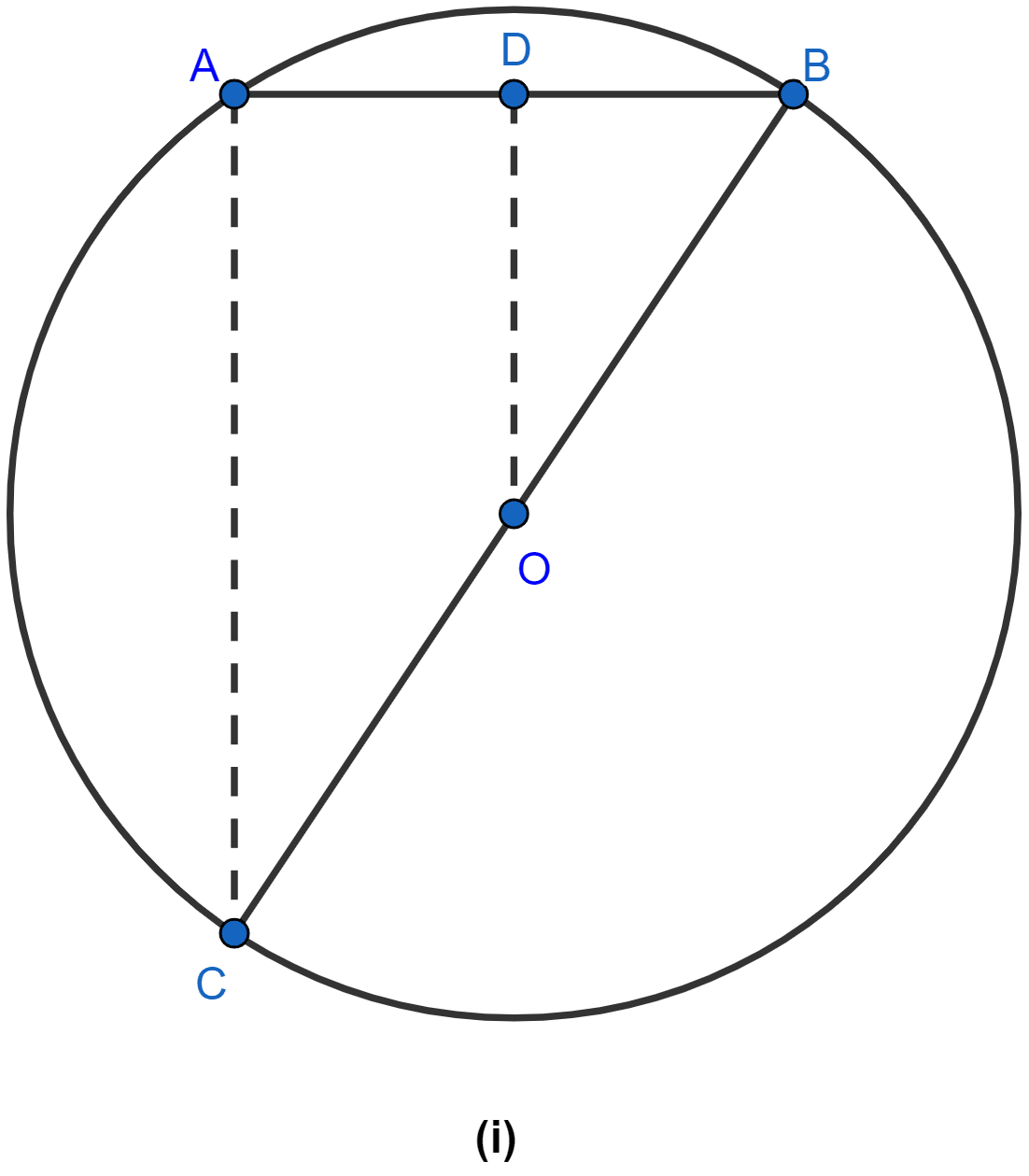
In the figure (ii) given below, O is the center of a circle. If AB and AC are chords of the circle such that AB = AC and OP ⊥ AB, OQ ⊥ AC, prove that PB = QC.