Mathematics
In △ABC, D is a point on BC such that AD is the bisector of ∠BAC. CE is drawn parallel to DA to meet BD produced at E. Prove that △CAE is isosceles.
Triangles
38 Likes
Answer
From figure,
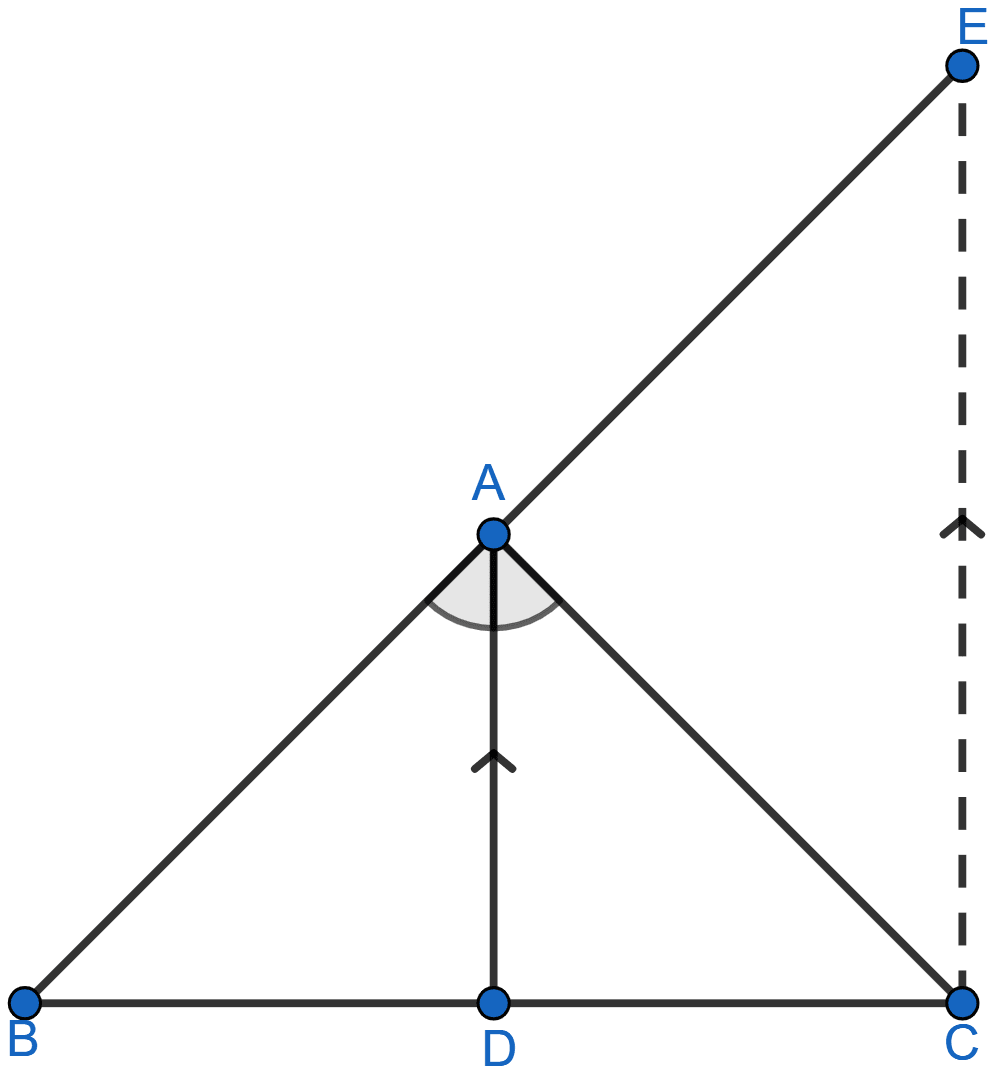
∠DAC= ∠ACE (Alternate angles)
∠BAD = ∠CEA (Corresponding angles)
But, ∠BAD = ∠DAC (as AD is bisector of ∠BAC)
∴ ∠ACE = ∠CEA
AE = AC (Sides opposite to equal angles are equal.)
∴ △CAE is isosceles triangle.
Hence, proved that △CAE is isosceles triangle.
Answered By
28 Likes
Related Questions
In the adjoining figure, BD= AD = AC. If ∠ABD = 36°, find the value of x.
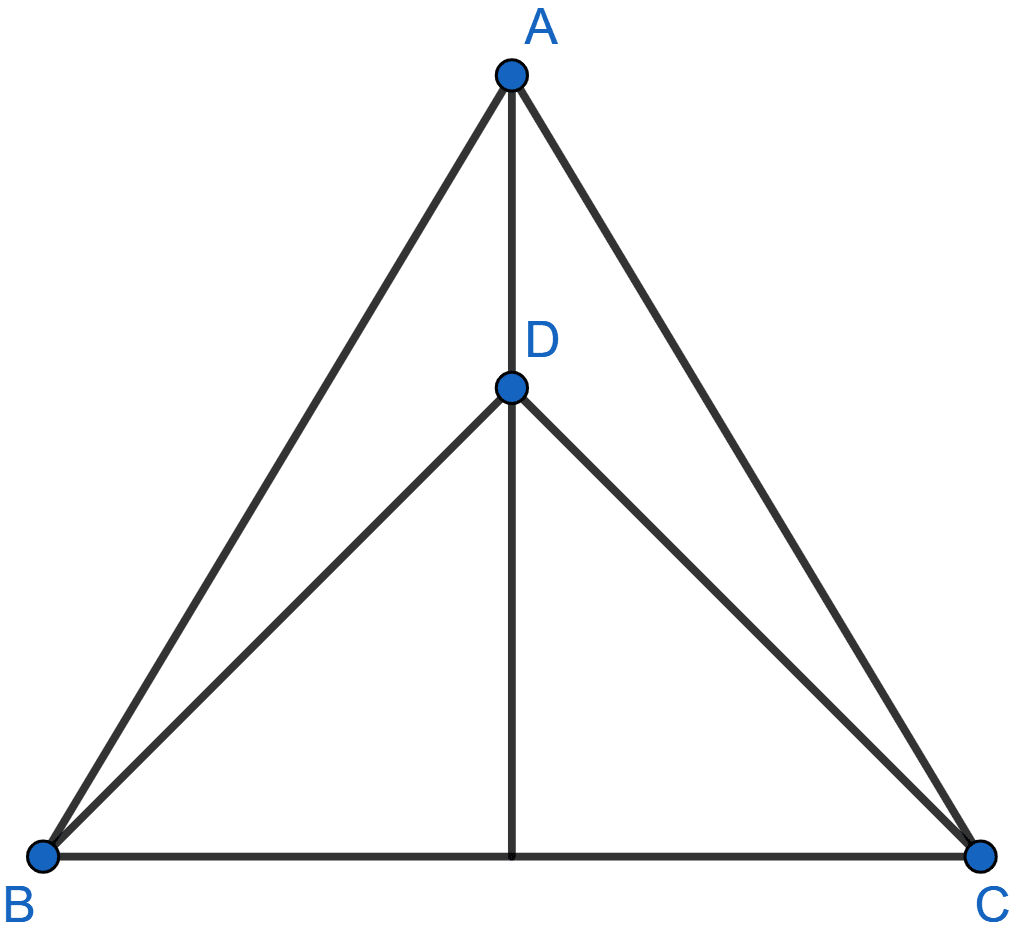
In the adjoining figure, AB = AC, D is a point in the interior of △ABC such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of △ABC.
In the adjoining figure, ABC is a right angled triangle at B. ADEC and BCFG are squares. Prove that AF = BE.
In the adjoining figure, AB || DC. CE and DE bisects ∠BCD and ∠ADC respectively. Prove that AB = AD + BC.
