Mathematics
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that :
(i) △PQL ~ △RPM
(ii) QL × RM = PL × PM
(iii) PQ2 = QR × QL
Related Questions
The line 3x - 4y + 12 = 0 meets x-axis at point A and y-axis at point B. Find :
(i) the coordinates of A and B.
(ii) equation of perpendicular bisector of line segment AB.
A straight line makes on the coordinate axes positive intercepts whose sum is 5. If the line passes through the point P(-3, 4), find its equation.
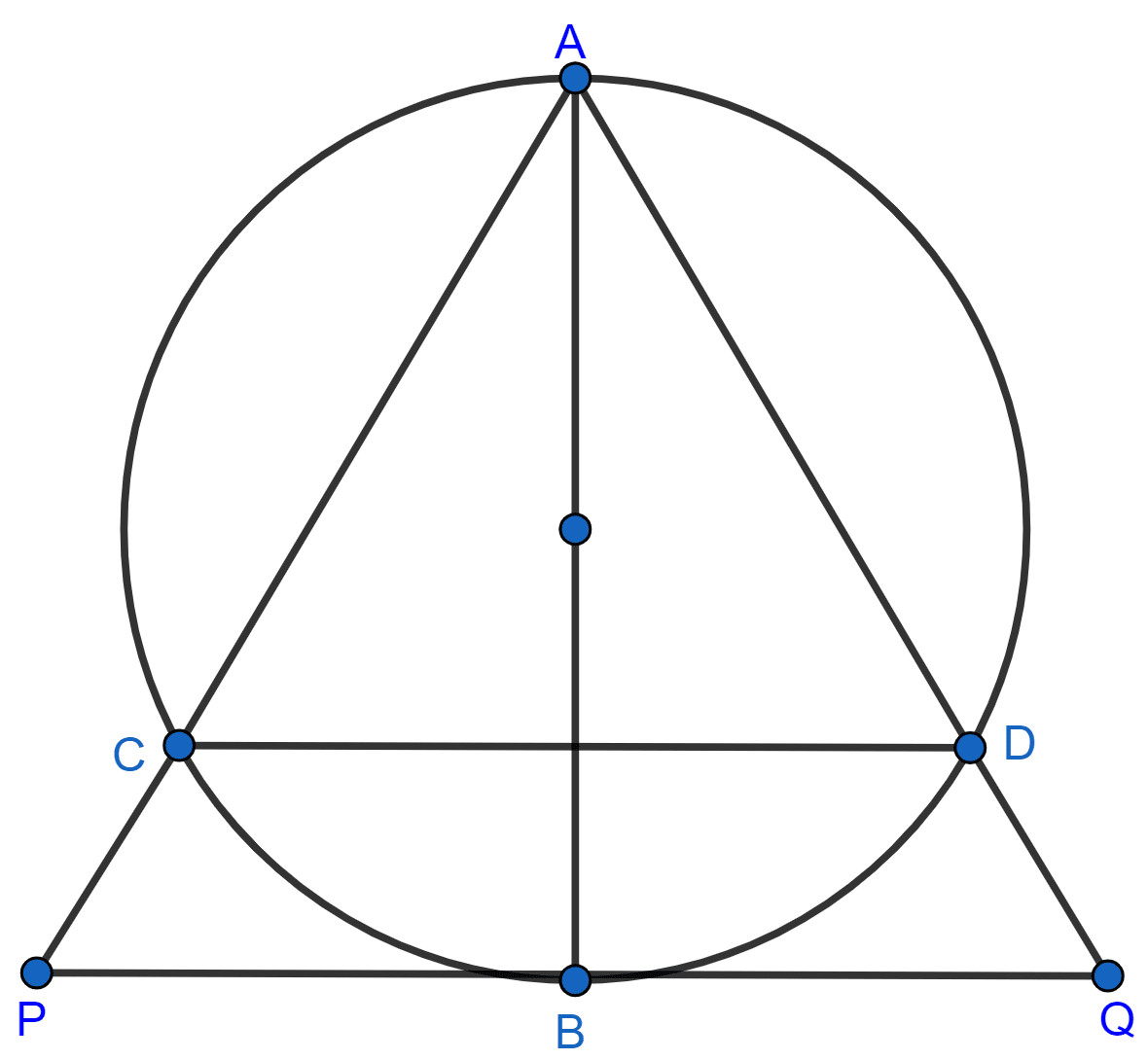
In the given figure, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that :
AB2 = AC × AP