Mathematics
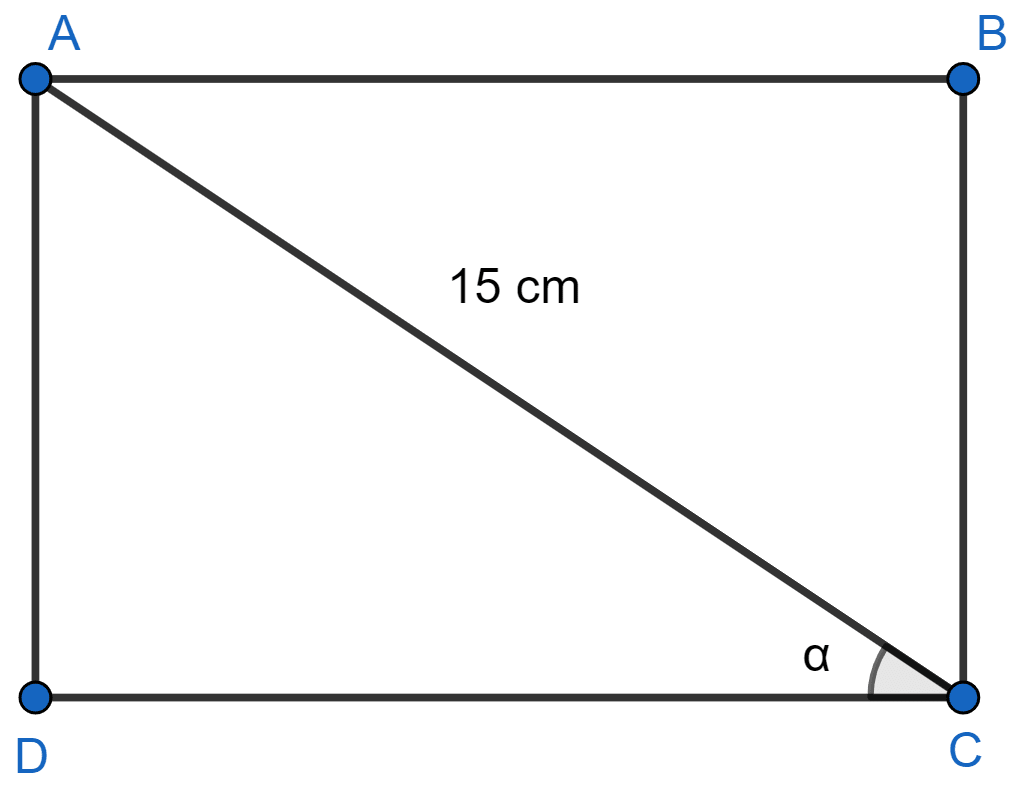
In a rectangle ABCD, its diagonal AC = 15 cm and ∠ACD = α. If cot α = , find the perimeter and the area of the rectangle.
Trigonometric Identities
Answer
Given,
cot α =
By formula,
⇒ cosec2 α = 1 + cot2 α
⇒ cosec2 α = 1 +
⇒ cosec2 α = 1 +
⇒ cosec2 α =
⇒ cosec2 α =
⇒ cosec α = .
By formula,
⇒ cosec α =
⇒ cosec α =
By formula,
⇒ cot α =
⇒ cot α =
Perimeter = 2(length + breadth) = 2(CD + AD)
=
=
=
= [Rationalising]
= cm.
Area = length × breadth
= CD × AD
= cm2.
Hence, perimeter = cm and area = cm2.
Answered By
Related Questions
The line 3x - 4y + 12 = 0 meets x-axis at point A and y-axis at point B. Find :
(i) the coordinates of A and B.
(ii) equation of perpendicular bisector of line segment AB.
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that :
(i) △PQL ~ △RPM
(ii) QL × RM = PL × PM
(iii) PQ2 = QR × QL
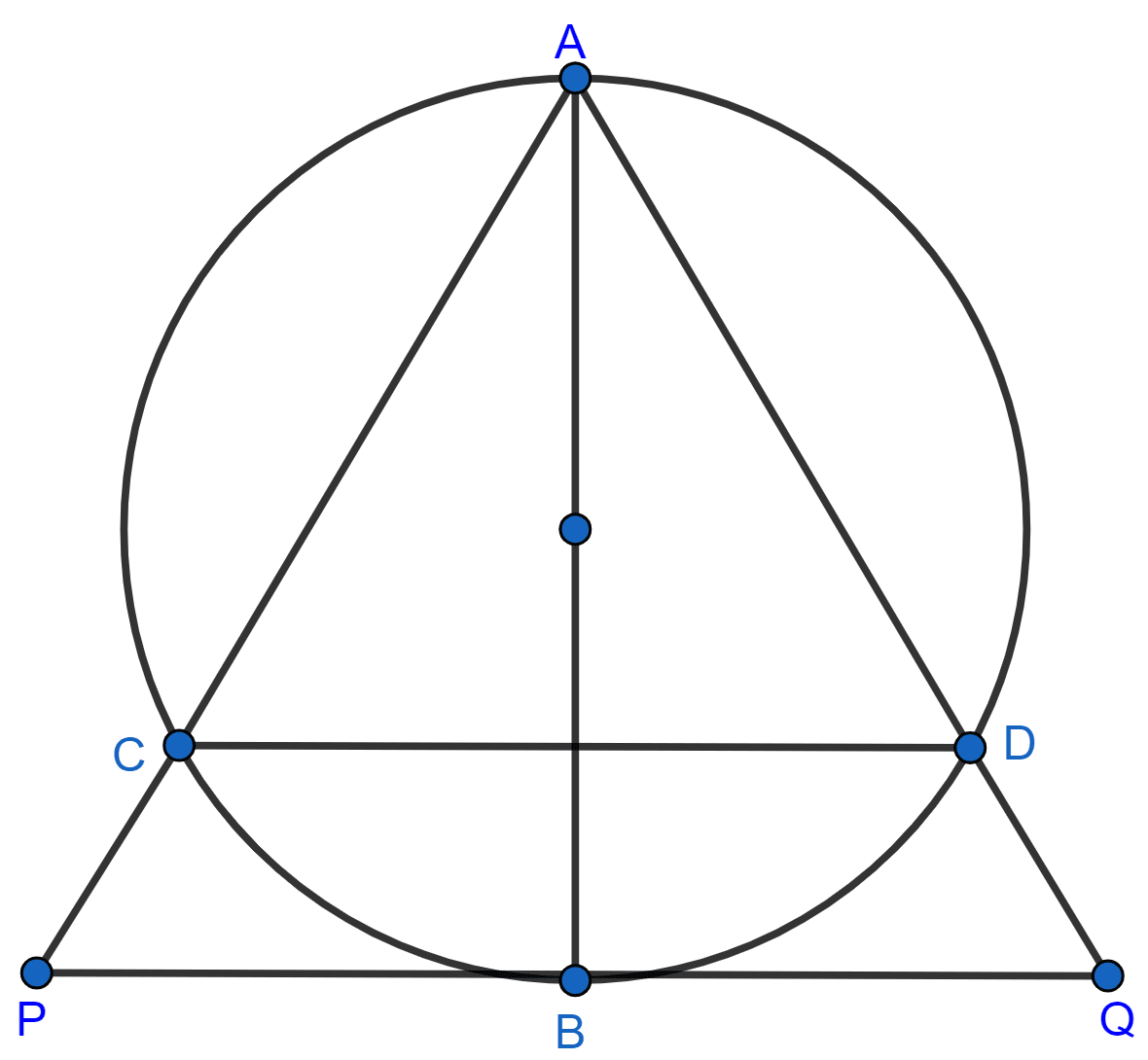
In the given figure, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that :
AB2 = AC × AP
Use ruler and compasses for this question.
(i) Construct an isosceles triangle ABC in which AB = AC = 7.5 cm and BC = 6 cm.
(ii) Draw AD, the perpendicular from vertex A to side BC.
(iii) Draw a circle with center A and radius 2.8 cm, cutting AD at E.
(iv) Construct another circle to circumscribe the triangle BCE.