Mathematics
In a quadrilateral ABCD, ∠B = 90° = ∠D. Prove that
2AC2 - BC2 = AB2 + AD2 + DC2.
Answer
Given, ∠B = 90° = ∠D
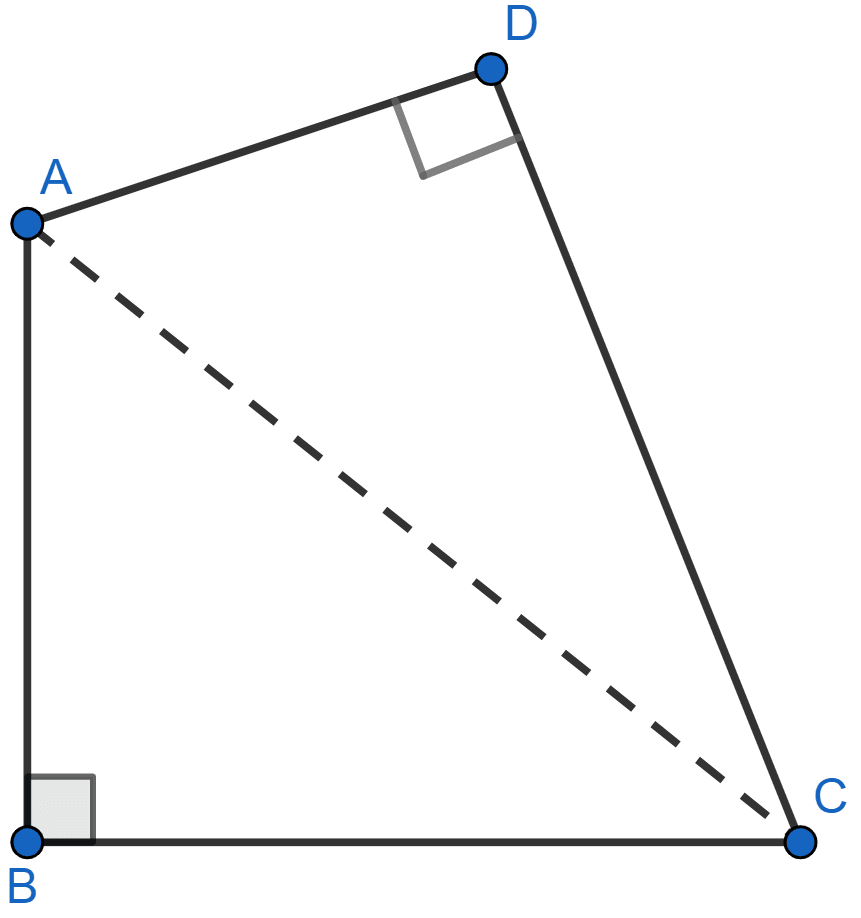
By pythagoras theorem,
In right angle triangle ABC,
AC2 = AB2 + BC2 ……(i)
By pythagoras theorem,
In right angle triangle ADC,
AC2 = AD2 + DC2 ……(ii)
Adding (i) and (ii) we get,
2AC2 = AB2 + BC2 + AD2 + DC2
2AC2 - BC2 = AB2 + AD2 + DC2.
Hence, proved that 2AC2 - BC2 = AB2 + AD2 + DC2.
Related Questions
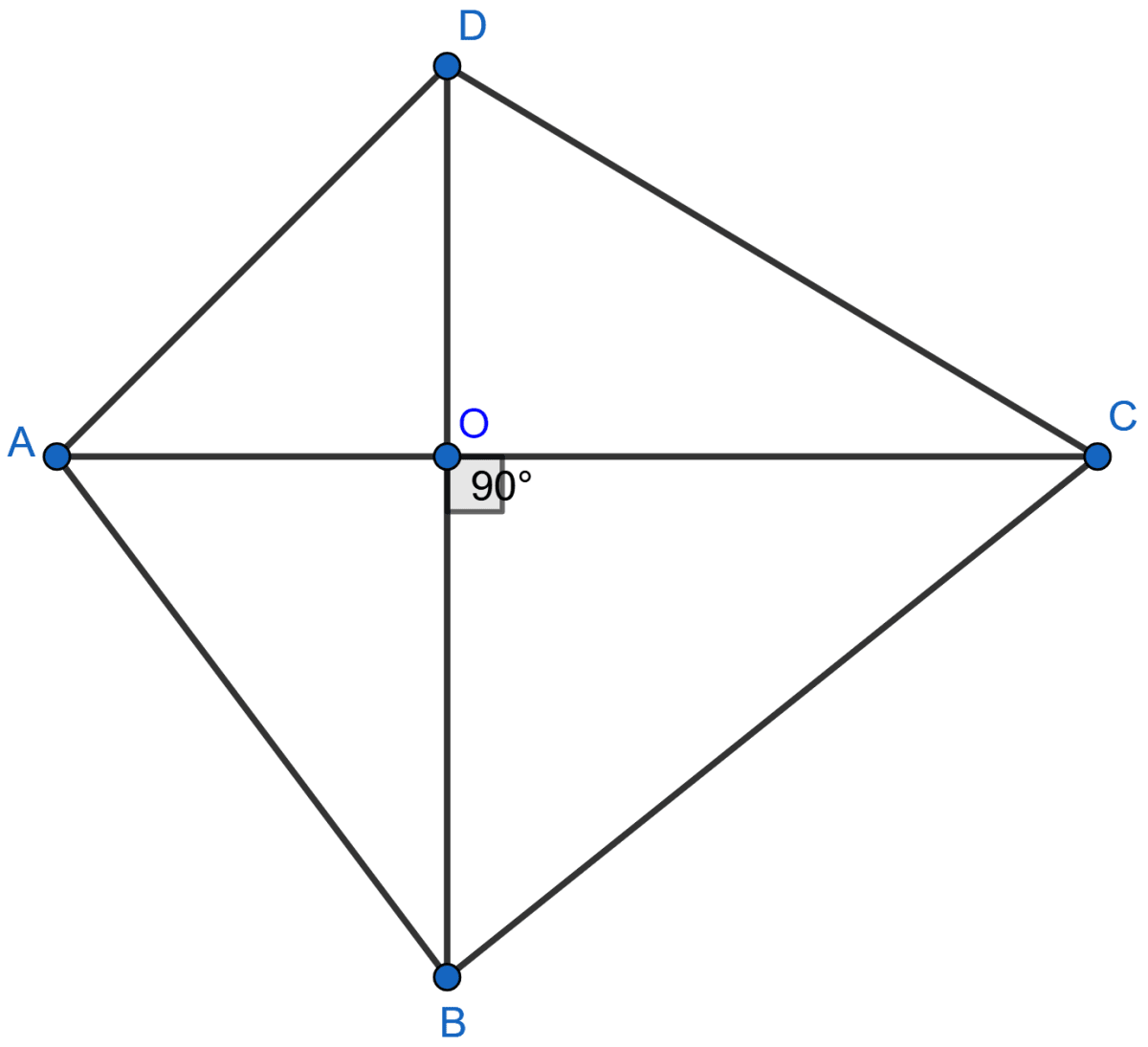
In the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O, at right angles. Prove that AB2 + CD2 = AD2 + BC2.
In a △ABC, ∠A = 90°, CA = AB and D is a point on AB produced. Prove that
DC2 - BD2 = 2AB × AD.
In an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that AD2 = AC2 + BD × CD.
If AD, BE and CF are medians of △ABC, prove that
3(AB2 + BC2 + CA2) = 4(AD2 + BE2 + CF2).