In an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that AD² = AC² + BD × CD.

Draw AP ⊥ BC.

APD is right triangle

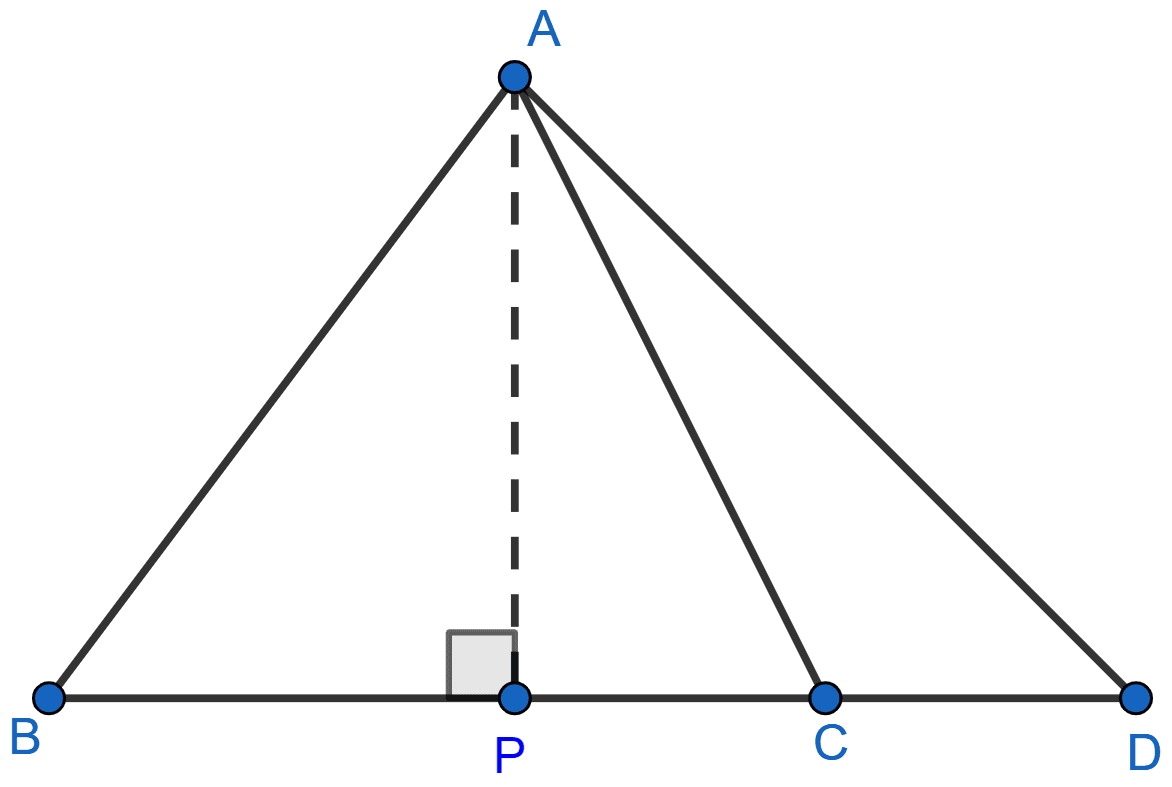
By pythagoras theorem we get,

⇒ AD² = AP² + PD²

⇒ AD² = AP² + (PC + CD)²

⇒ AD² = AP² + PC² + CD² + 2PC.CD ……(i)

APC is right triangle,

By pythagoras theorem we get,

⇒ AC² = AP² + PC² ……(ii)

Substituting the value of AP² + PC² from (ii) in (i) we get,

⇒ AD² = AC² + CD² + 2PC.CD …….(iii)

Since, ABC is an isosceles triangle,

⇒ PC = $\dfrac{\text{BC}}{2}$ [∵ altitude to the base of an isosceles triangle bisects the base]

⇒ AD² = AC² + CD² + $2 \times \dfrac{1}{2} \times \text{BC} \times \text{CD}$

⇒ AD² = AC² + CD² + BC.CD

⇒ AD² = AC² + CD(CD + BC)

From figure, CD + BC = BD

⇒ AD² = AC² + CD.BD

Hence, proved that AD² = AC² + BD × CD.