Mathematics
In a quadrilateral ABCD, AB = AD and CB = CD. Prove that :
(i) AC bisects angle BAD.
(ii) AC is perpendicular bisector of BD.
Related Questions
ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ; prove that AP and DQ are perpendicular to each other.
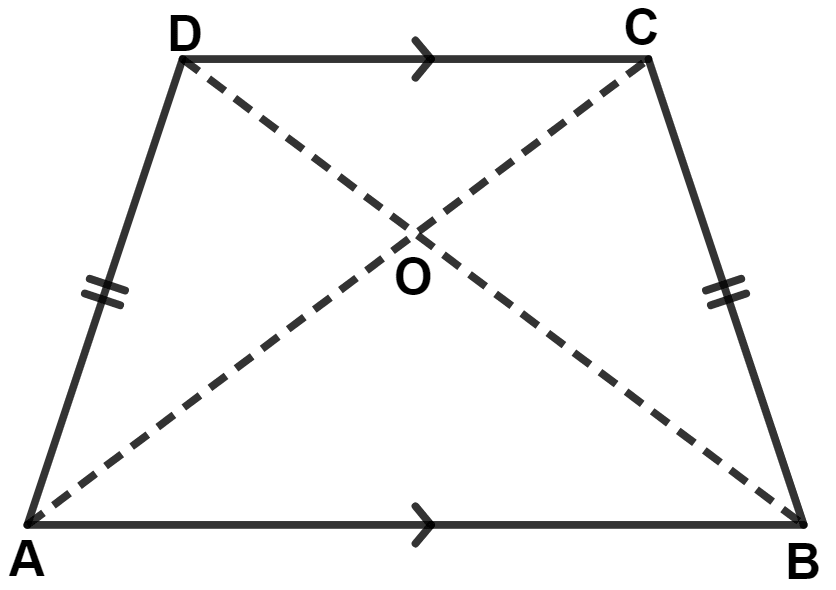
The following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC.
Prove that :
(i) ∠DAB = ∠CBA
(ii) ∠ADC = ∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
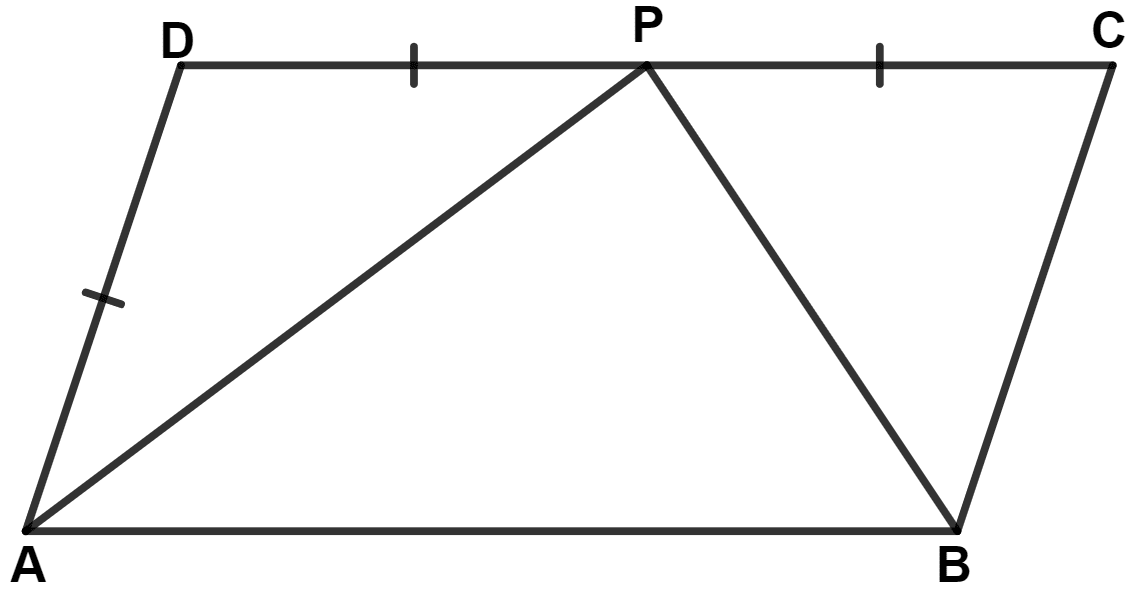
In the following figure, ABCD is a parallelogram. Prove that :
(i) AP bisects angle A
(ii) BP bisects angle B
(iii) ∠DAP + ∠CBP = ∠APB