Mathematics
In a quadrilateral ABCD, AB = AD and CB = CD. Prove that :
(i) AC bisects angle BAD.
(ii) AC is perpendicular bisector of BD.
Rectilinear Figures
Answer

(i) In △ ABC and △ ADC,
⇒ AB = AD (Given)
⇒ BC = CD (Given)
⇒ AC = AC (Common side)
∴ △ ABC ≅ △ ADC (By S.S.S. axiom)
We know that,
Corresponding parts of congruent triangle are equal.
⇒ ∠BAC = ∠DAC
∴ AC bisects ∠BAD.
Hence, proved that AC bisects angle BAD.
(ii) Since, AC bisects ∠BAD
∴ ∠BAO = ∠DAO
In △ AOB and △ AOD,
⇒ AB = AD (Given)
⇒ AO = AO (Common side)
⇒ ∠BAO = ∠DAO (Proved above)
∴ △ AOB ≅ △ AOD (By S.A.S. axiom)
We know that,
Corresponding parts of congruent triangle are equal.
⇒ ∠BOA = ∠DOA ……..(1)
From figure,
⇒ ∠BOA + ∠DOA = 180° (Linear pair)
⇒ ∠BOA + ∠BOA = 180° [From equation (1)]
⇒ 2∠BOA = 180°
⇒ ∠BOA = = 90°.
∴ AC is perpendicular bisector of BD.
Hence, proved that AC is perpendicular bisector of BD.
Answered By
Related Questions
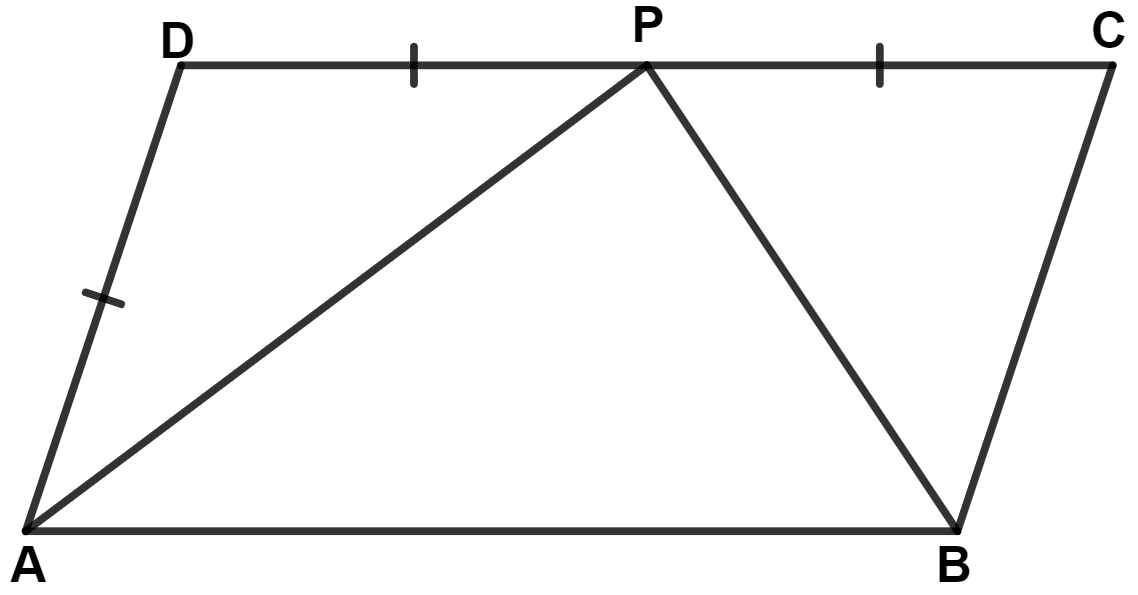
In the following figure, ABCD is a parallelogram. Prove that :
(i) AP bisects angle A
(ii) BP bisects angle B
(iii) ∠DAP + ∠CBP = ∠APB
ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ; prove that AP and DQ are perpendicular to each other.
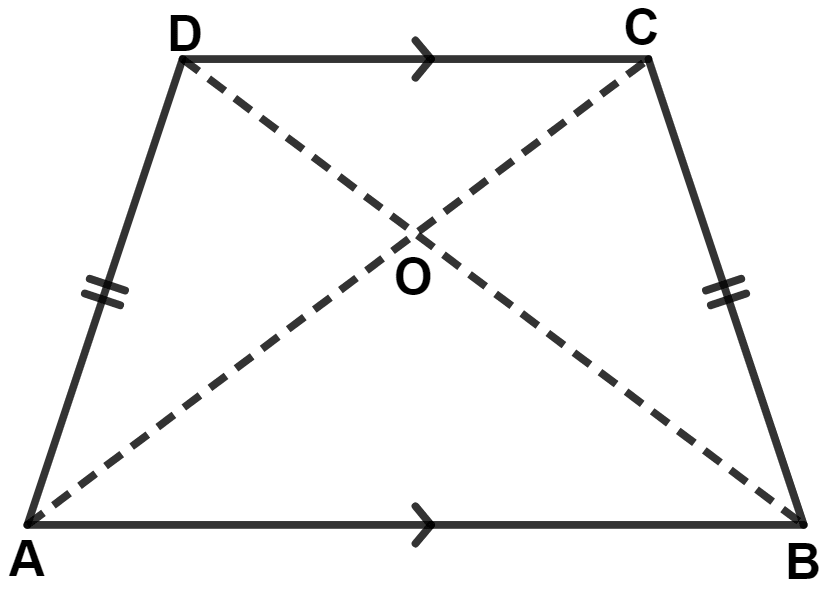
The following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC.
Prove that :
(i) ∠DAB = ∠CBA
(ii) ∠ADC = ∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD
The difference between an exterior angle of (n - 1) sided regular polygon and an exterior angle of (n + 2) sided regular polygon is 6°. Find the value of n.