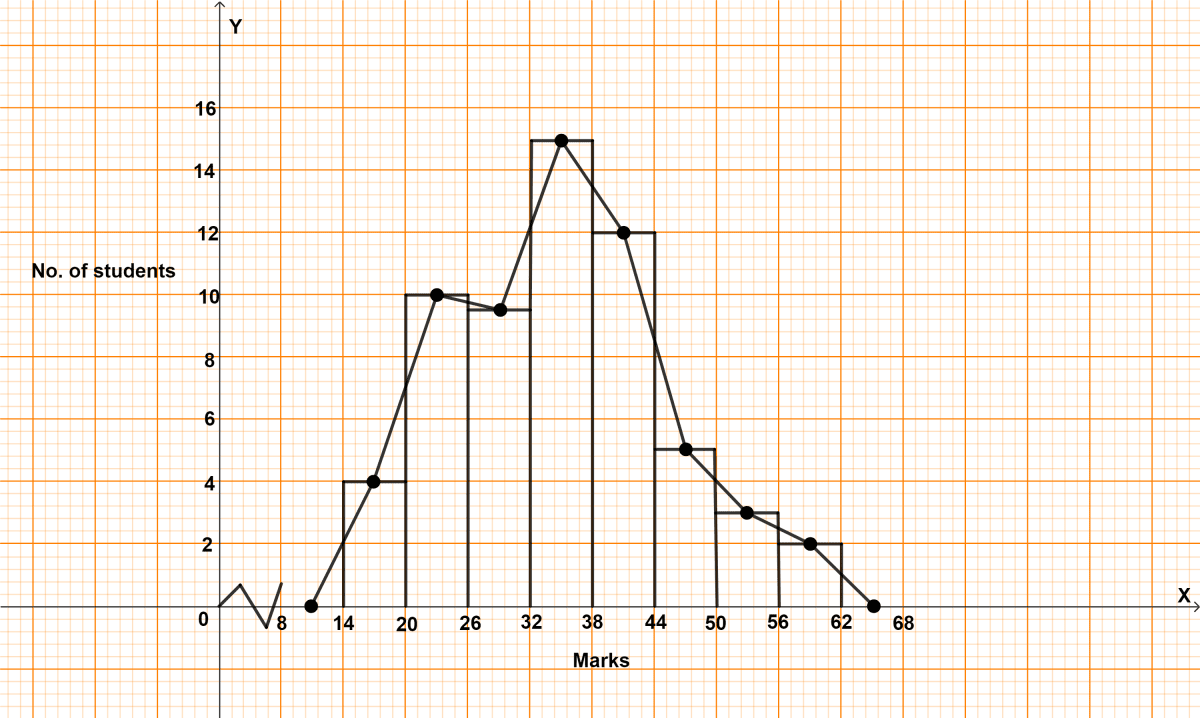
In a class of 60 students, the marks obtained in a surprise test were as under :

Marks	No. of students
14 - 20	4
20 - 26	10
26 - 32	9
32 - 38	15
38 - 44	12
44 - 50	5
50 - 56	3
56 - 62	2

Represent the above data by a histogram and a frequency polygon.

Steps of construction of histogram :

1. Since, the scale on x-axis starts at 8, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 8.

2. Take 1 cm along x-axis = 10 marks.

3. Take 1 cm along y-axis = 5 students.

4. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Steps of construction of frequency polygon :

1. Mark the mid-points of upper bases of rectangles of the histogram.

2. Join the consecutive mid-points by line segments.

3. Join the first end point with the mid-point of class 8 - 14 with zero frequency, and join the other end point with the mid-point of class 62 - 68 wirh zero frequency.

The required frequency polygon is shown by thick line segments in the diagram.