Mathematics

Construct a combined histogram and frequency polygon for the following distribution:
Classes Frequency
91 - 100 16
101 - 110 28
111 - 120 44
121 - 130 20
131 - 140 32
141 - 150 12
151 - 160 4

6 Likes

The following frequency distribution is discontinuous, to convert it into continuous frequency distribution,

Adjustment factor = (Lower limit of one class - Upper limit of previous class) / 2

= $\dfrac{101 - 100}{2} = \dfrac{1}{2}$

= 0.5

Subtract the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.

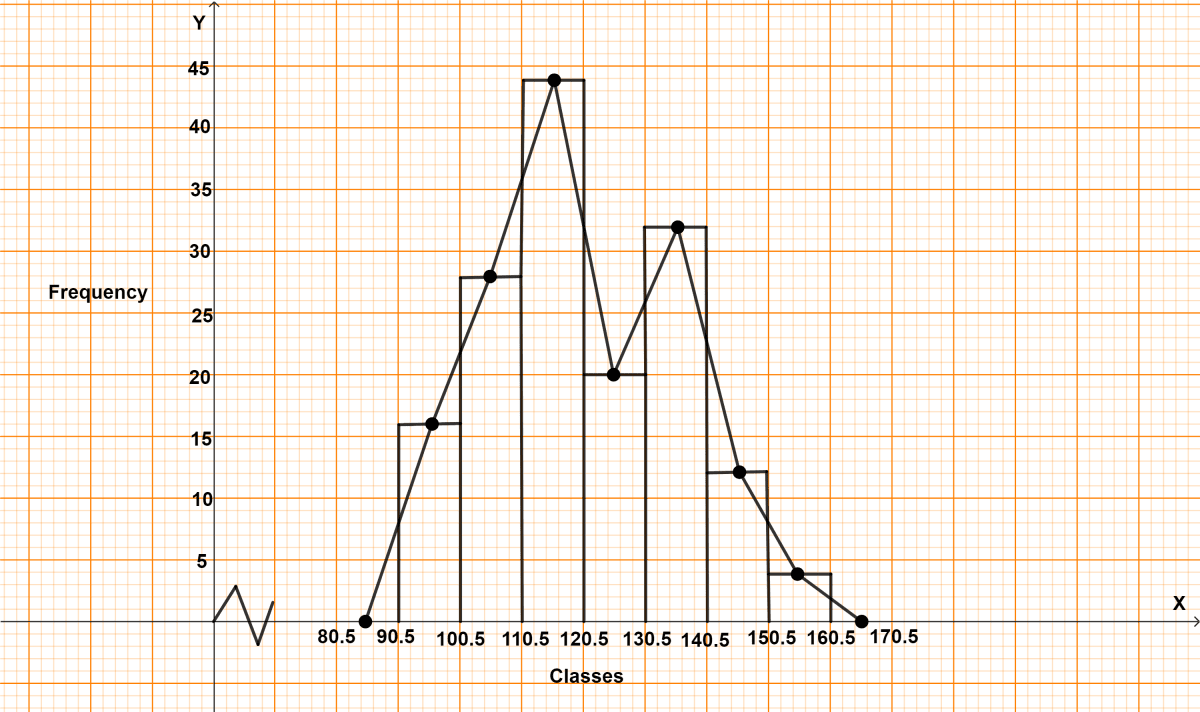
Continuous frequency distribution for given data is :

Classes before adjustment	Classes after adjustment	Class mark	Frequency
91 - 100	90.5 - 100.5	95.5	16
101 - 110	100.5 - 110.5	105.5	28
111 - 120	110.5 - 120.5	115.5	44
121 - 130	120.5 - 130.5	125.5	20
131 - 140	130.5 - 140.5	135.5	32
141 - 150	140.5 - 150.5	145.5	12
151 - 160	150.5 - 160.5	155.5	4

Steps of construction of histogram :

Since, the scale on x-axis starts at 80.5, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 80.5
Take 1 cm along x-axis = 10 units.
Take 1 cm along y-axis = 5 units.
Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Steps of construction of frequency polygon :

Mark the mid-points of upper bases of rectangles of the histogram.
Join the consecutive mid-points by line segments.
Join the first end point with the mid-point of class 80.5 - 90.5 with zero frequency, and join the other end point with the mid-point of class 160.5 - 170.5 with zero frequency.

The required frequency polygon is shown by thick line segments in the diagram.

Answered By

3 Likes