Mathematics
In a circle of radius 5 cm, AB and CD are two parallel chords of length 8 cm and 6 cm respectively. Calculate the distance between the chords, if they are on
(i) the same side of the centre
(ii) the opposite sides of the centre.
Related Questions
A chord of length 16 cm is at a distance 6 cm from the center of the circle. Find the length of chord of the same circle which is at a distance of 8 cm from the center.
In figure (i) given below, O is the center of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) radius of the circle
(ii) length of chord CD.
Calculate the length of a chord which is at a distance 6 cm from the center of a circle of diameter 20 cm.
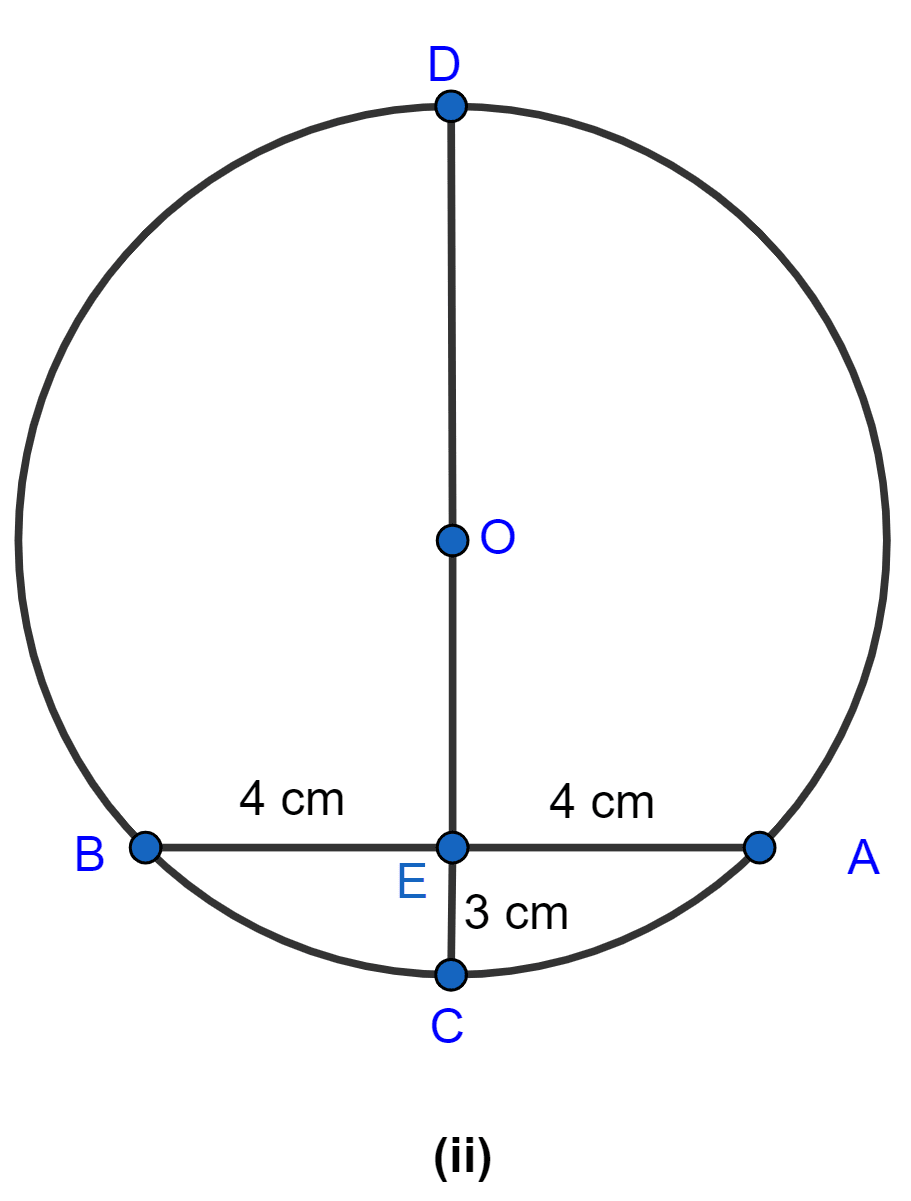
In the figure (ii) given below, CD is the diameter which meets the chord AB in E such that AE = BE = 4 cm. If CE = 3 cm, find the radius of the circle.
