Mathematics
In a △ABC, D and E are points on the sides AB and AC respectively such that AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and AC = 8.8 cm. Is DE || BC? Justify your answer.
Similarity
8 Likes
Answer
EC = AC - AE = 8.8 - 3.3 = 5.5 cm.
Calculating ,
So, .
Hence, by basic proportionality theorem DE || BC.
Answered By
6 Likes
Related Questions
In the given figure, P is a point on AB such that PB : AP = 3 : 4 and PQ || AC.
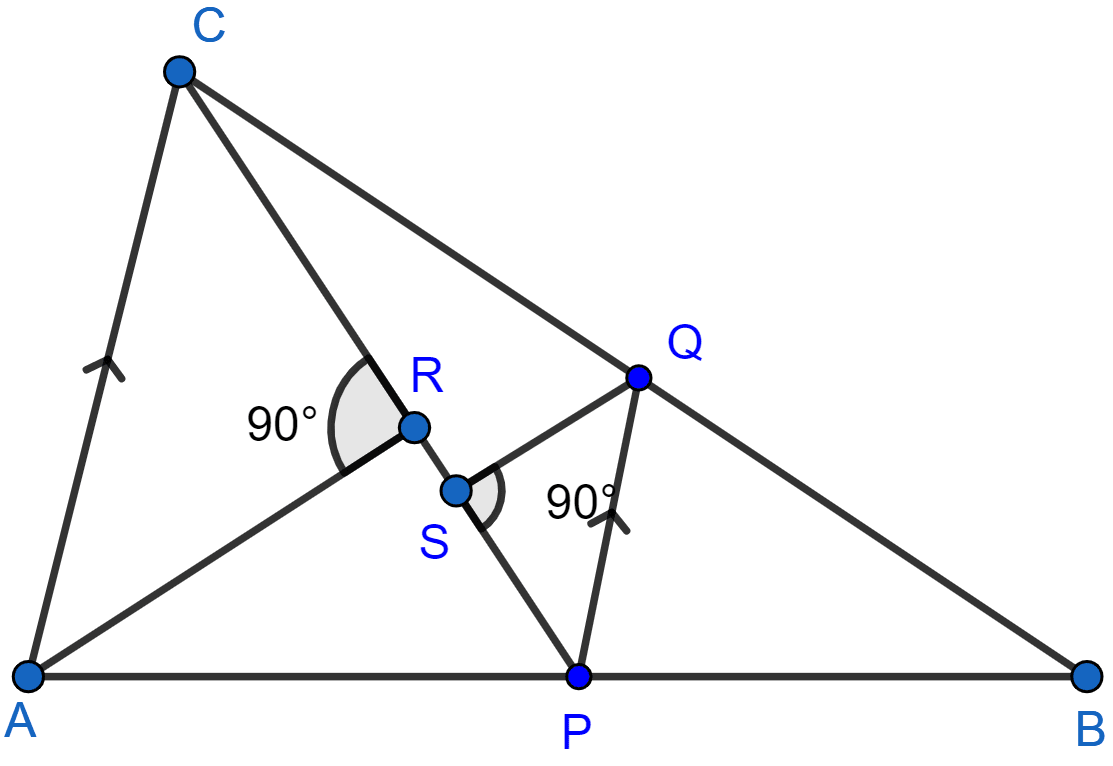
(i) Calculate PQ : AC.
(ii) If AR ⊥ CP, QS ⊥ CB and QS = 6 cm, calculate the length of AR.
In a △ABC, D and E are points on the sides AB and AC respectively such that DE || BC. If AD = 2.4 cm, AE = 3.2 cm, DE = 2 cm and BC = 5 cm, find BD and CE.
If the areas of two similar triangles are 360 cm2 and 250 cm2 and if one side of the first triangle is 8 cm, find the length of the corresponding side of the second triangle.
In the adjoining figure, D is a point on BC such that ∠ABD = ∠CAD. If AB = 5 cm, AC = 3 cm and AD = 4 cm, find
(i) BC
(ii) DC
(iii) area of △ACD : area of △BCA
