Mathematics
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Answer
Let O be the center of circle, with AB and CD as equal chords.
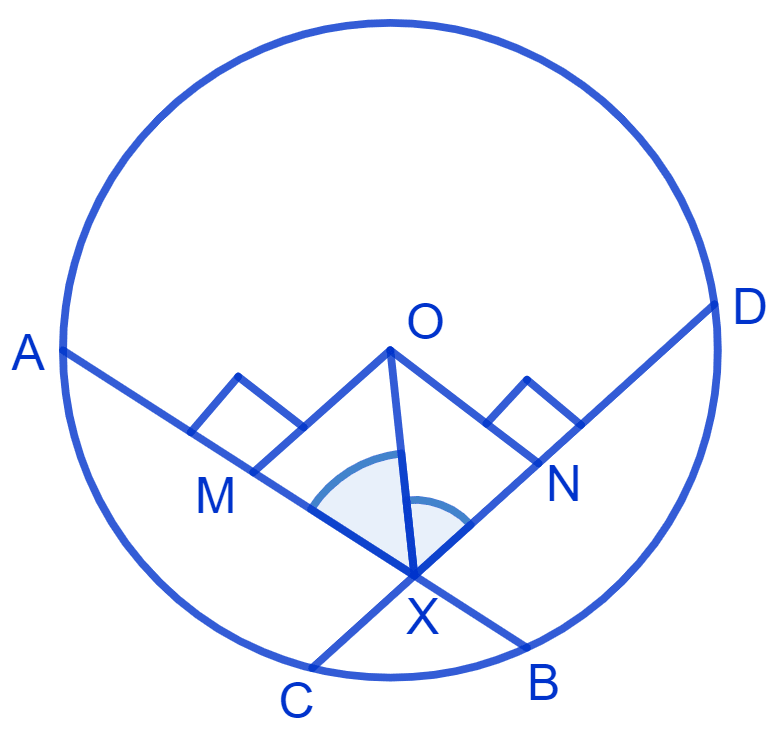
From figure,
X is the point of intersection from the chords.
Draw OM ⊥ AB and ON ⊥ CD.
In ∆ OMX and ∆ ONX,
⇒ ∠OMX = ∠ONX = 90°
⇒ OX = OX (Common)
We know that,
AB and CD are equal chords and equal chords are equidistant from the centre.
⇒ OM = ON
⇒ ∆ OMX ≅ ∆ ONX (By R.H.S. congruence rule)
⇒ ∠OXM = ∠OXN (By C.P.C.T.)
⇒ ∠OXA = ∠OXD
Hence, proved that the line joining the point of intersection to the centre makes equal angles with the chords.
Related Questions
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD.
Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?