Mathematics
If the sides of a rectangle touch a circle, prove that the rectangle is a square.
Circles
23 Likes
Answer
The figure below shows a rectangle ABCD with its sides touching the circle at points P, Q, R and S.
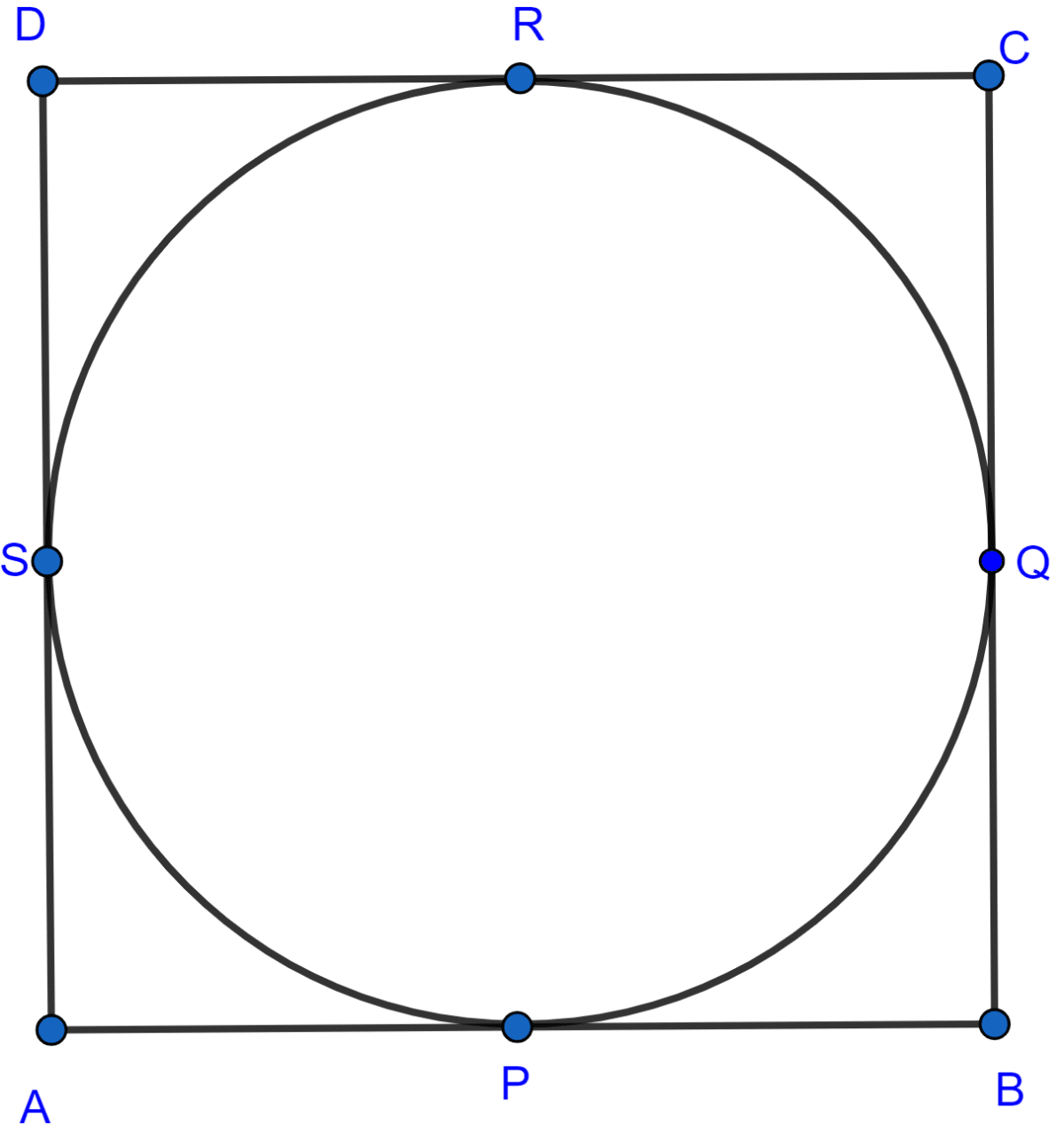
We know that,
Length of tangents from an external point to the circle are equal.
Hence,
AP = AS …..(Eq. 1)
BP = BQ …..(Eq. 2)
CR = CQ …..(Eq. 3)
DR = DS …..(Eq. 4)
Adding the above 4 equations,
⇒ AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ AB + CD = AD + BC
But AB = CD and AD = BC (As opposite sides of a rectangle are equal.)
⇒ AB + AB = BC + BC
⇒ 2AB = 2BC
⇒ AB = BC.
∴ AB = BC = CD = DA.
Hence, proved that ABCD is a square.
Answered By
15 Likes
Related Questions
In the adjoining figure, △ABC is isosceles with AB = AC. Prove that the tangent at A to the circumcircle of △ABC is parallel to BC.

In the figure (ii) given below, two circles with centres C, C' intersect at A, B and the point C lies on the circle with C'. PQ is a tangent to the circle with centre C' at A. Prove that AC bisects ∠PAB.

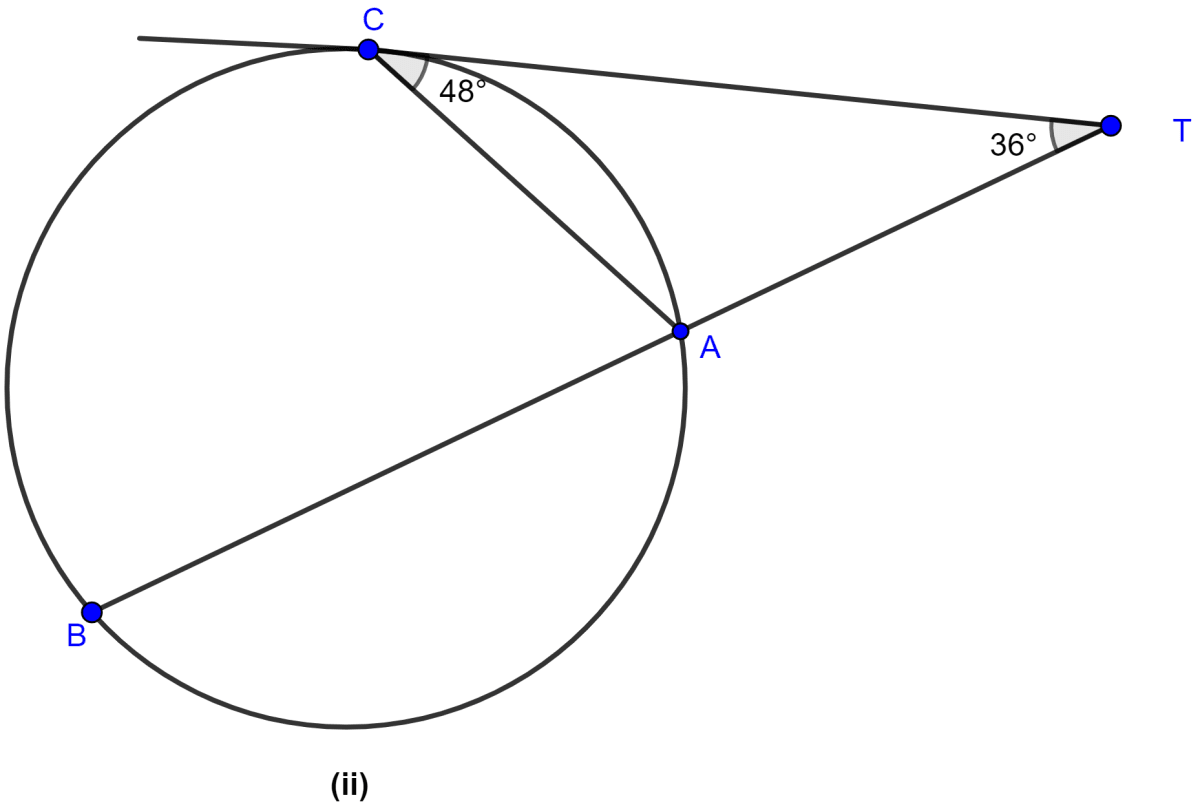
In the figure (ii) given below, A, B and C are three points on a circle. The tangent at C meets BA produced at T. Given that ∠ATC = 36° and ∠ACT = 48°, calculate the angle subtended by AB at the centre of the circle.
In the figure (i) given below, two circles intersect at A, B. From a point P on one of these circles, two line segments PAC and PBD are drawn, intersecting the other circles at C and D respectively. Prove that CD is parallel to the tangent at P.
