Mathematics
If the diagonals of a square ABCD intersect each other at O, then △OAB is
an equilateral triangle
a right angled but not an isosceles triangle
an isosceles but not right angles triangle
an isosceles right angled triangle.
Rectilinear Figures
Answer
Since, diagonals of square bisect each other at 90°.
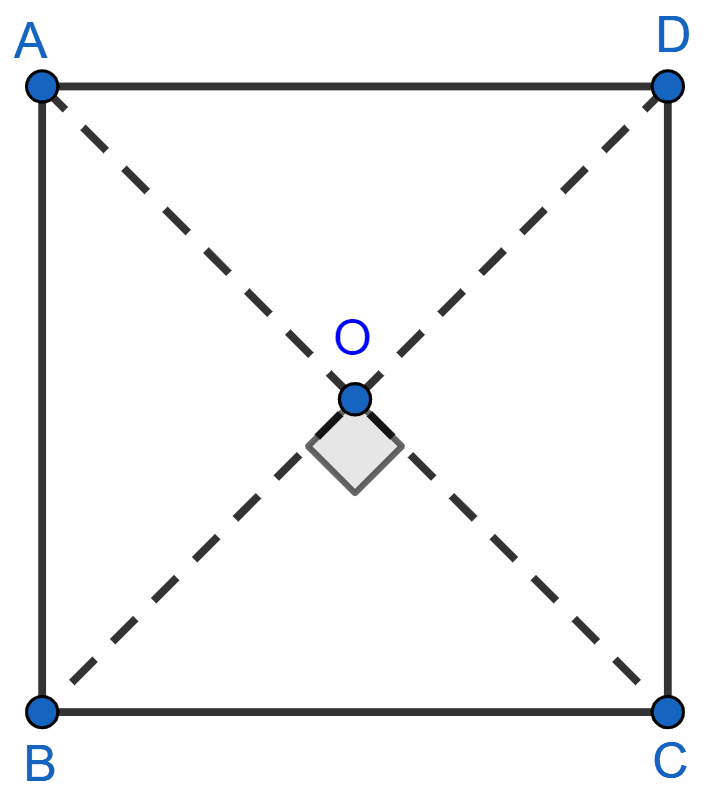
In △OAB,
AO = OB and ∠AOB = 90°.
Hence, it is an isosceles right angled triangle.
Hence, Option 4 is the correct option.
Answered By
Related Questions
ABCD is a rhombus such that ∠ACB = 40°. Then ∠ADB is
40°
45°
50°
60°
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC = 32° and ∠AOB = 70°, then ∠DBC is equal to
24°
86°
38°
32°
If the diagonals of a quadrilateral PQRS bisect each other, then the quadrilateral PQRS must be a
parallelogram
rhombus
rectangle
square
If the diagonals of a quadrilateral PQRS bisect each other at right angles, then the quadrilateral PQRS must be a
parallelogram
rectangle
rhombus
square