Mathematics
ABCD is a rhombus such that ∠ACB = 40°. Then ∠ADB is
40°
45°
50°
60°
Rectilinear Figures
4 Likes
Answer
From figure,
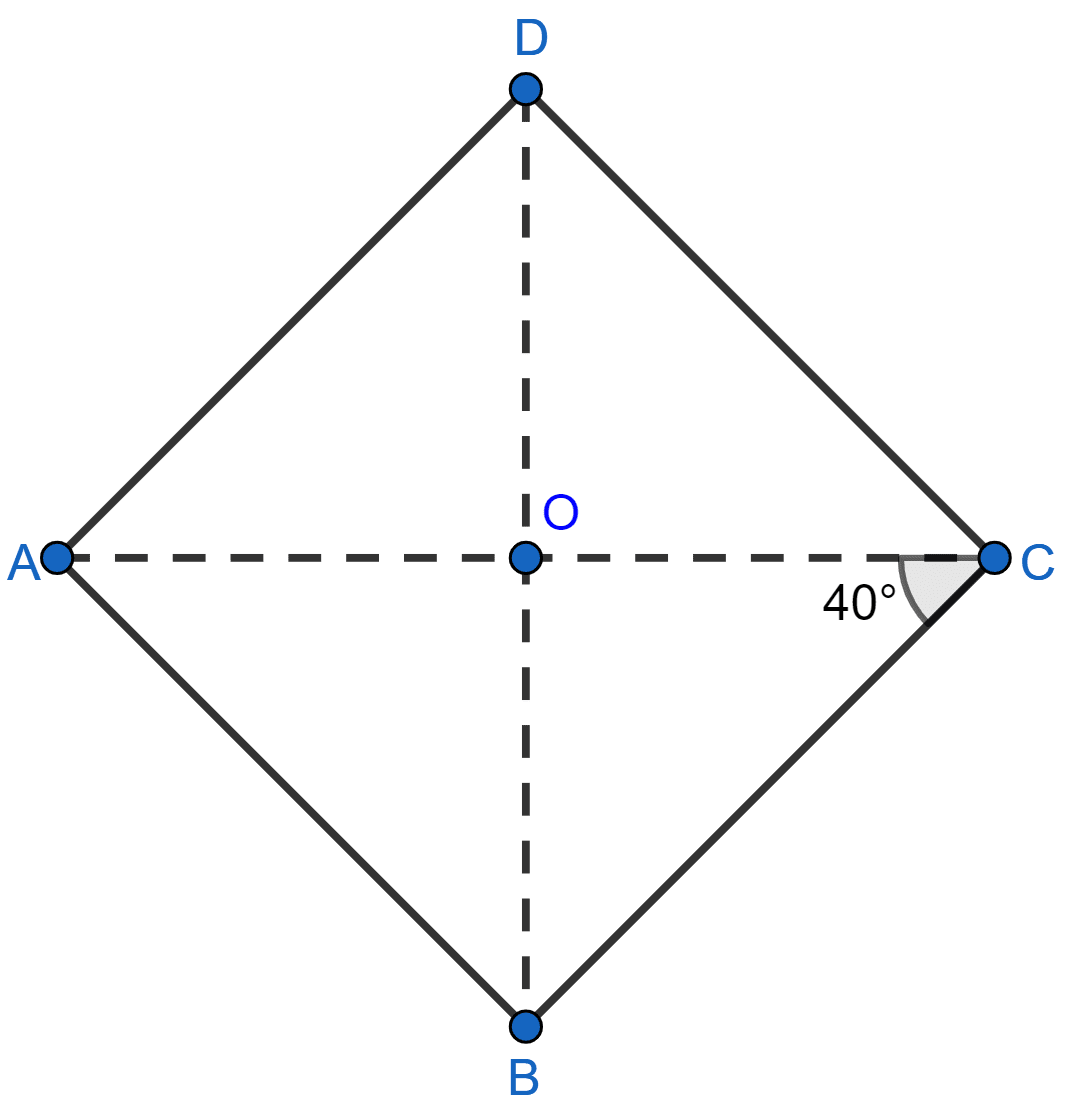
⇒ ∠DAO = ∠OCB = 40° (Alternate angles are equal.)
In △ADO,
⇒ ∠DAO + ∠AOD + ∠ODA = 180°
⇒ 40° + 90° + ∠ODA = 180°
⇒ ∠ODA = 180° - 130° = 50°.
From figure,
∠ADB = ∠ODA = 50°.
Hence, Option 3 is the correct option.
Answered By
3 Likes
Related Questions
If PQRS is a parallelogram, then ∠Q - ∠S is equal to
90°
120°
0°
180°
A diagonal of a rectangle is inclined to one side of the rectangle at 25°. The acute angle between the diagonals is
55°
50°
40°
25°
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC = 32° and ∠AOB = 70°, then ∠DBC is equal to
24°
86°
38°
32°
If the diagonals of a square ABCD intersect each other at O, then △OAB is
an equilateral triangle
a right angled but not an isosceles triangle
an isosceles but not right angles triangle
an isosceles right angled triangle.