Mathematics
If the diagonals of a square ABCD intersect each other at O, then △OAB is
an equilateral triangle
a right angled but not an isosceles triangle
an isosceles but not right angles triangle
an isosceles right angled triangle.
Rectilinear Figures
1 Like
Answer
Since, diagonals of square bisect each other at 90°.
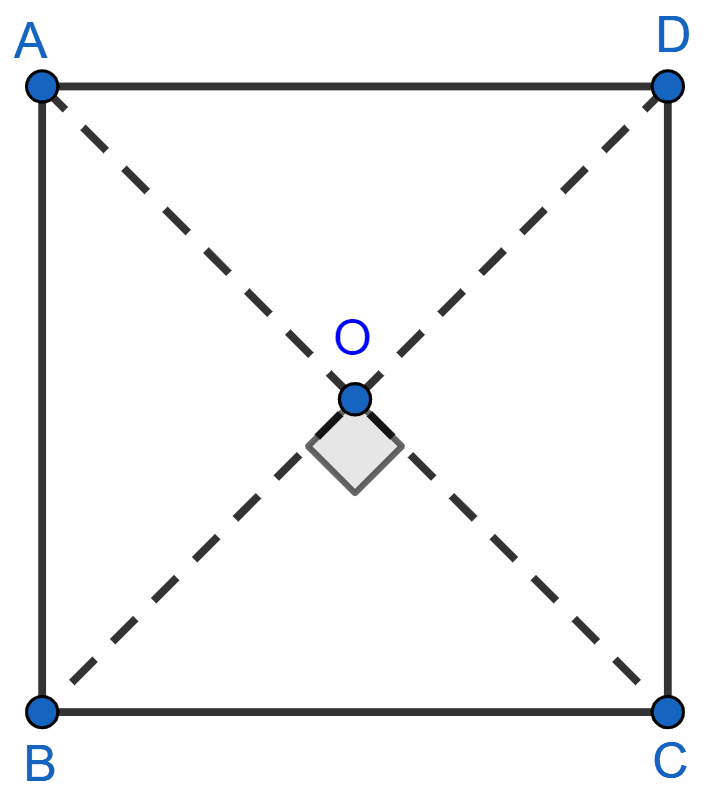
In △OAB,
AO = OB and ∠AOB = 90°.
Hence, it is an isosceles right angled triangle.
Hence, Option 4 is the correct option.
Answered By
1 Like
Related Questions
ABCD is a rhombus such that ∠ACB = 40°. Then ∠ADB is
40°
45°
50°
60°
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC = 32° and ∠AOB = 70°, then ∠DBC is equal to
24°
86°
38°
32°
If the diagonals of a quadrilateral PQRS bisect each other, then the quadrilateral PQRS must be a
parallelogram
rhombus
rectangle
square
If the diagonals of a quadrilateral PQRS bisect each other at right angles, then the quadrilateral PQRS must be a
parallelogram
rectangle
rhombus
square