Mathematics
If tangents PA and PB from a point P to a circle with center O are inclined to each other at angle of 80°, then ∠POA is equal to
50°
60°
70°
80°
Circles
2 Likes
Answer
We know that,
The lengths of tangents drawn from an external point to a circle are equal.
A tangent at any point of a circle is perpendicular to the radius at the point of contact.
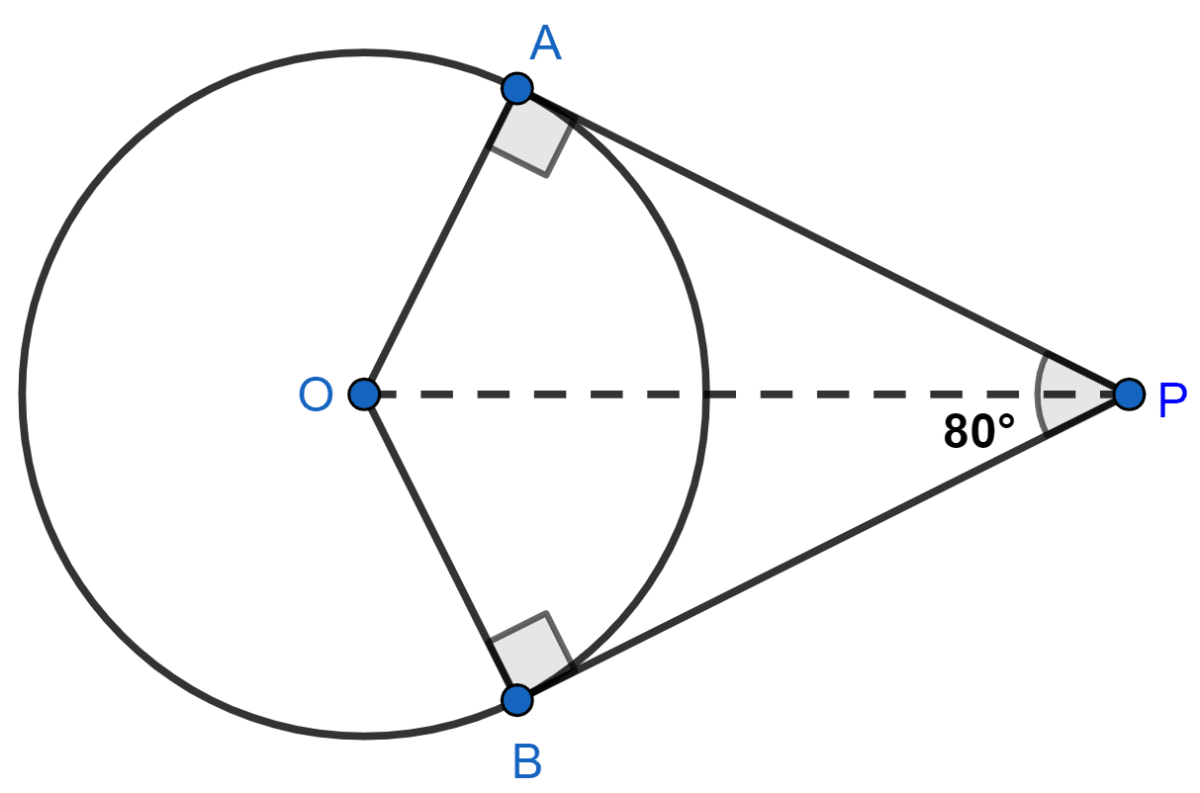
In Δ OAP and Δ OBP,
⇒ OA = OB (radii of the circle are always equal)
⇒ AP = BP (length of the tangents)
⇒ OP = OP (common)
Therefore, by SSS congruency Δ OAP ≅ Δ OBP
Also,
By C.P.C.T.,
⇒ ∠POA = ∠POB
⇒ ∠OPA = ∠OPB
Therefore, OP is the angle bisector of ∠APB and ∠AOB.
Hence, ∠OPA = ∠OPB = ∠APB
= × 80°
= 40°.
In Δ OAP
We know that,
OA ⊥ AP ( The tangent at any point of a circle is perpendicular to the radius through the point of contact.)
∴ ∠OAP = 90°.
By angle sum property of a triangle,
⇒ ∠OAP + ∠POA + ∠OPA = 180°
⇒ 90° + ∠POA + 40° = 180°
⇒ 130° + ∠POA = 180°
⇒ ∠POA = 180° - 130°
⇒ ∠POA = 50°.
Hence, Option 1 is the correct option.
Answered By
3 Likes
Related Questions
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
7 cm
12 cm
15 cm
24.5 cm
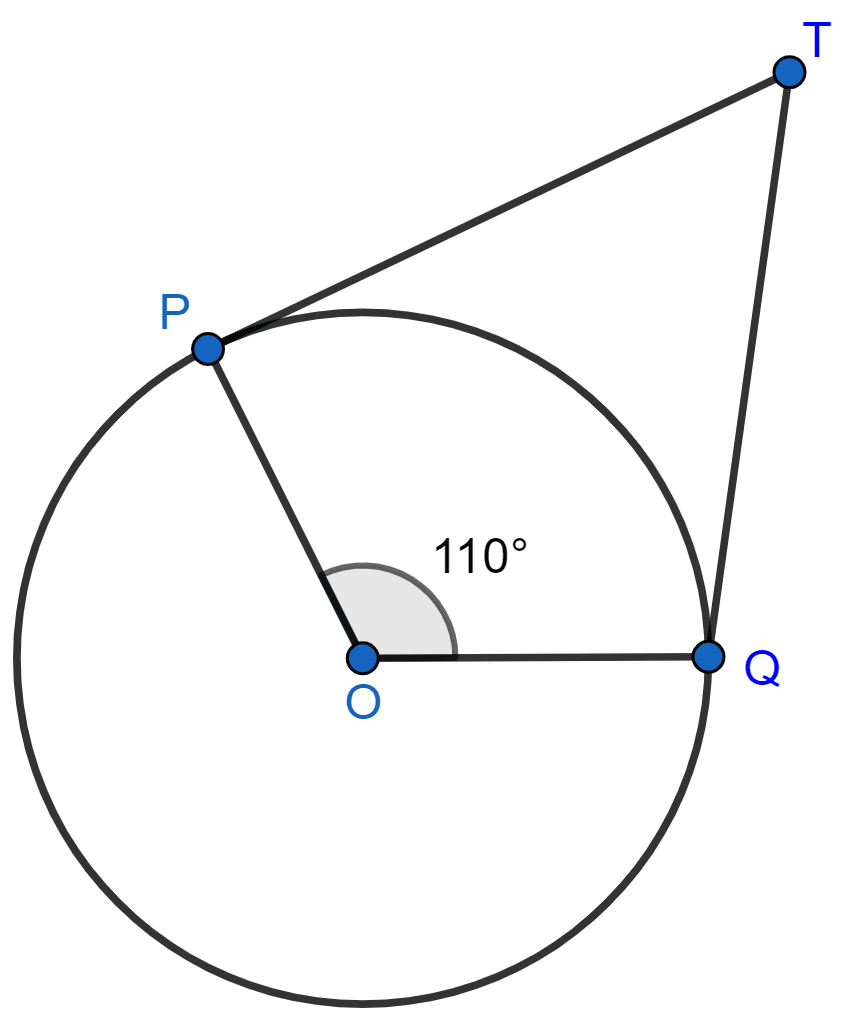
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
60°
70°
80°
90°
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.