Mathematics
If P'(-4, -3) is the image of a point P under reflection in the origin, find
(i) the coordinates of P.
(ii) the coordinates of the image of P under reflection in the line y = -2.
Reflection
26 Likes
Answer
(i) Since, P'(-4, -3) is the image of P under reflection in the origin, from graph P(4, 3).
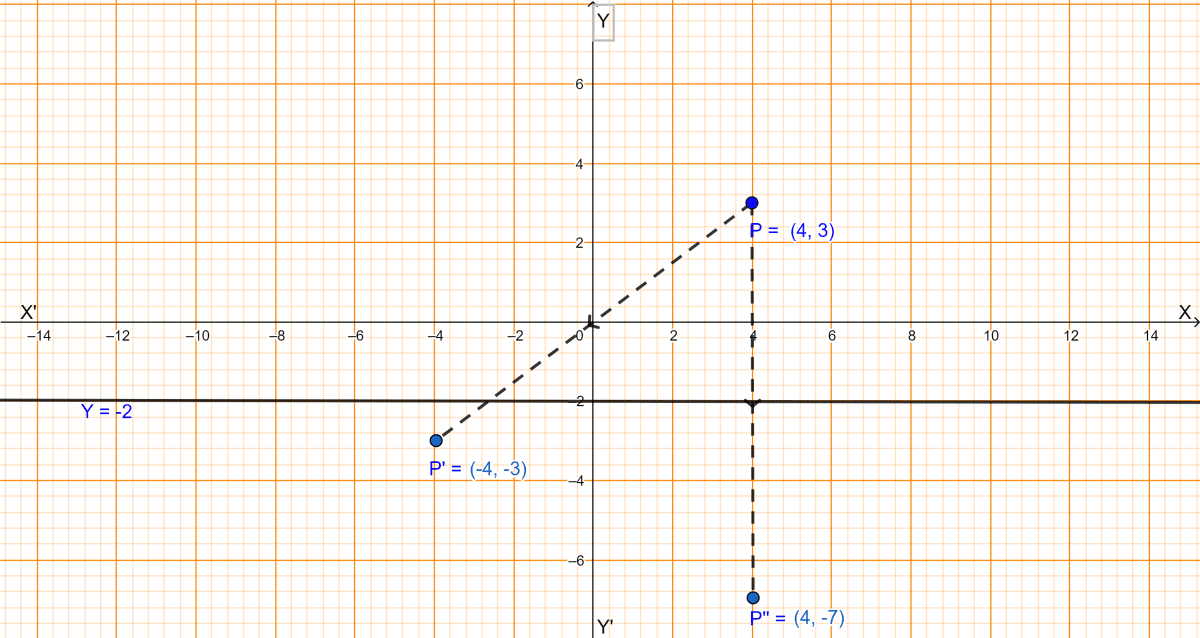
Hence, the coordinates of P are (4, 3).
(ii) We know that the reflection of the point (x, y) in the line y = a is the point (x, -y + 2a).
∴ The image of the point P(4, 3) under reflection in the line y = -2 is the point P''(4, -(3) + 2 × (-2)) i.e., the point P''(4, -7).
Hence, the coordinates of P under reflection in the line y = -2 is (4, -7).
Answered By
22 Likes
Related Questions
Write down the coordinates of the image of the point (3, -2) when:
(i) reflected in the x-axis.
(ii) reflected in the y-axis.
(iii) reflected in the x-axis followed by reflection in the y-axis.
(iv) reflected in the origin.
Find the coordinates of the image of (3, 1) under reflection in x-axis followed by reflection in the line x = 1.
A point P(a, b) is reflected in the x-axis to P'(2, -3), write down the values of a and b. P'' is the image of P, when reflected in the y-axis. Write down the coordinates of P''. Find the coordinates of P''', when P is reflected in the line, parallel to y-axis such that x = 4.
(i) Point P(a, b) is reflected in the x-axis to P'(5, -2). Write down the values of a and b.
(ii) P'' is the image of P when reflected in the y-axis. Write down the coordinates of P''.
(iii) Name a single transformation that maps P' into P''.