Write down the coordinates of the image of the point (3, -2) when:

(i) reflected in the x-axis.

(ii) reflected in the y-axis.

(iii) reflected in the x-axis followed by reflection in the y-axis.

(iv) reflected in the origin.

(i) We know that,

Rule to find reflection of a point in x-axis :

1. Retain the abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point P'(3, 2) is the image on reflection.

Hence, (3, 2) is the image of the point (3, -2) on reflection in x-axis.

(ii) We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

∴ Point P'(-3, -2) is the image on reflection.

Hence, (-3, -2) is the image of the point (3, -2) on reflection in y-axis.

(iii) On reflection in x-axis the point P(3, -2) becomes P'(3, 2) which on further reflection in y-axis becomes P''(-3, 2) as shown in the graph.

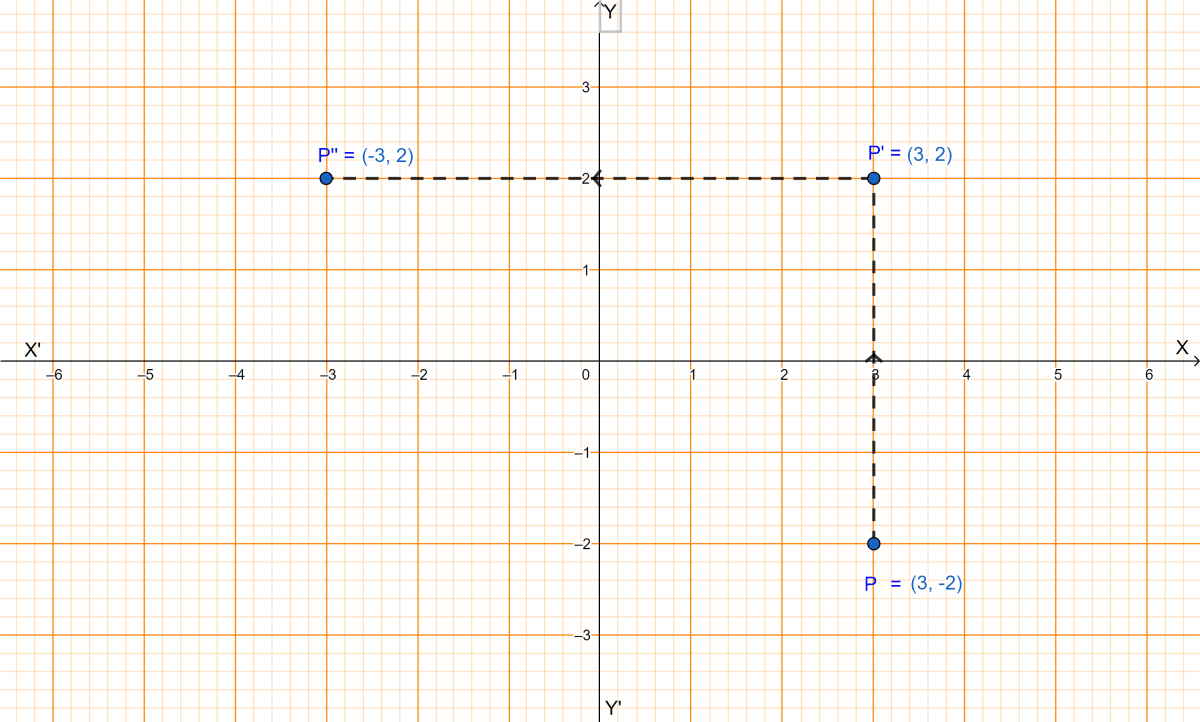
Hence, P''(-3, 2) is the final image after reflections.

(iv) We know that,

Rules to find the reflection of a point in the origin :

1. Change the sign of abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point P'(-3, 2) is the image on reflection.

Hence, (-3, 2) is the image of the point (3, -2) on reflection in origin.