Mathematics
If P and Q are points of trisection of the diagonal BD of a parallelogram ABCD, prove that CQ || AP.
Rectilinear Figures
15 Likes
Answer
Since, AB || CD (Opposite sides of parallelogram are parallel) and BD is transversal.
From figure,
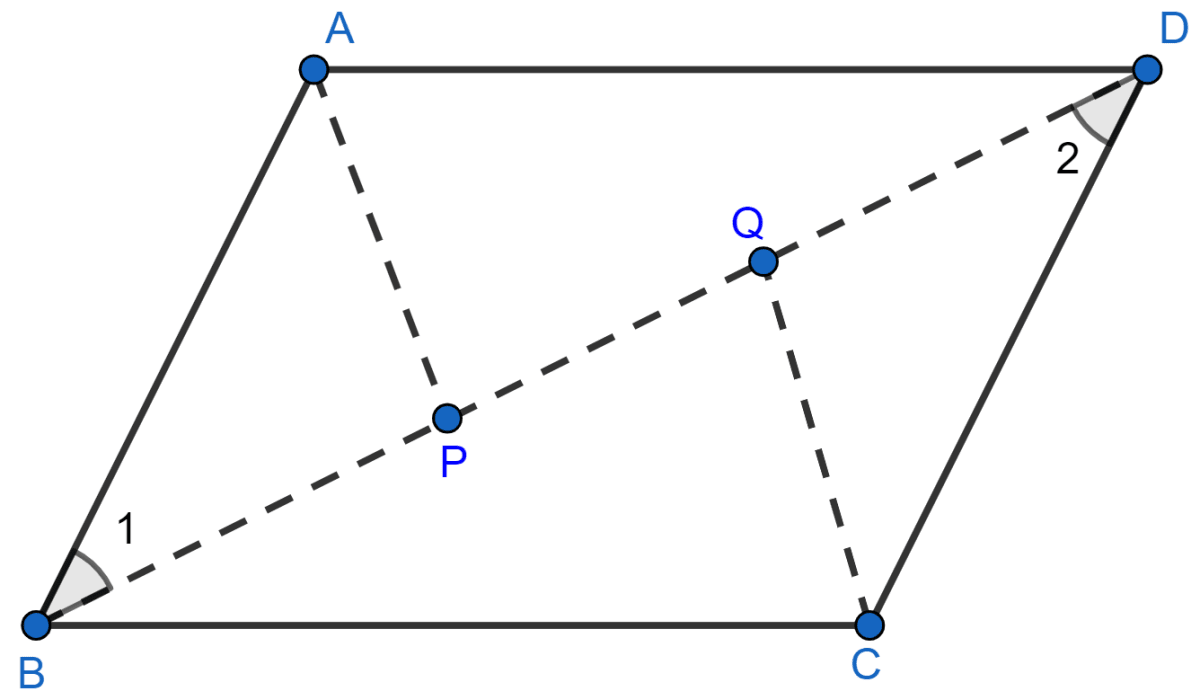
∠ABP = ∠CDQ (Alternate angles are equal)
BP = QD (As P and Q are points of trisection of the diagonal BD)
AB = CD (Opposite sides of parallelogram are equal)
Hence, △ABP ≅ △CDQ by SAS axiom.
∴ ∠APB = ∠CQD …….(By C.P.C.T.)
Multiplying both sides by -1
-∠APB = -∠CQD
Adding 180° on both sides,
⇒ 180° - ∠APB = 180° -∠CQD
⇒ ∠APQ = ∠CQP
The above angles are alternate angles and since they are equal we can say,
AP || CQ.
Hence, proved that AP || CQ.
Answered By
12 Likes
Related Questions
In figure (2) given below, points P and Q have been taken on opposite sides AB and CD respectively of a parallelogram ABCD such that AP = CQ. Show that AC and PQ bisect each other.
A transversal cuts two parallel lines at A and B. The two interior angles at A are bisected and so are the two interior angles at B; the four bisectors form a quadrilateral ACBD. Prove that
(i) ACBD is a rectangle.
(ii) CD is parallel to the original parallel lines.
ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ, prove that AP and DQ are perpendicular to each other.
In parallelogram ABCD, the bisector of ∠A meets DC in E and AB = 2AD. Prove that
(i) BE bisects ∠B
(ii) ∠AEB = a right angle.