Mathematics
A transversal cuts two parallel lines at A and B. The two interior angles at A are bisected and so are the two interior angles at B; the four bisectors form a quadrilateral ACBD. Prove that
(i) ACBD is a rectangle.
(ii) CD is parallel to the original parallel lines.
Rectilinear Figures
100 Likes
Answer
From figure,
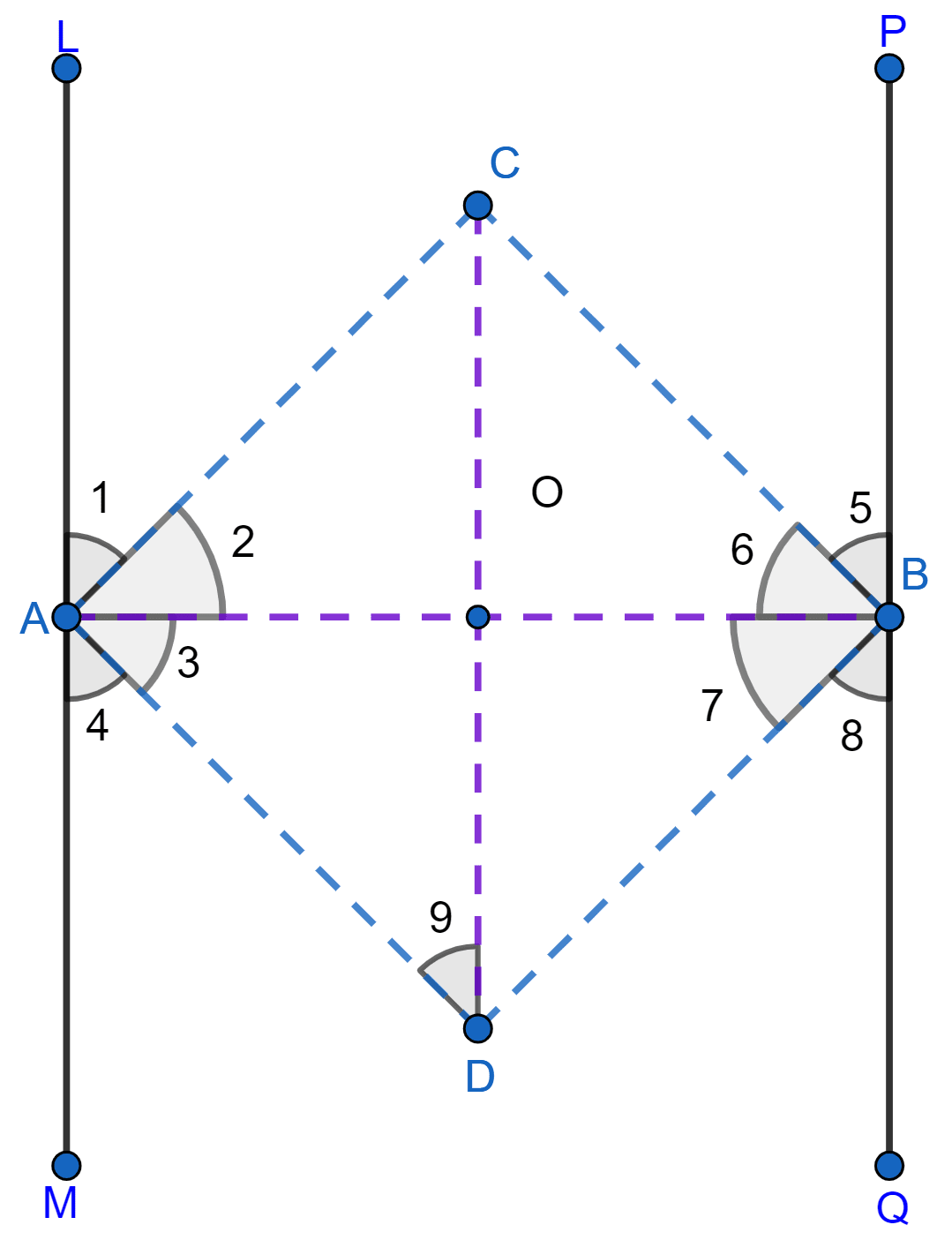
LM || PQ and AB is transversal.
AC, AD, BC and BD are bisectors of ∠LAB, ∠BAM, ∠PBA and ∠ABQ respectively.
So,
∠1 = ∠2, ∠3 = ∠4, ∠5 = ∠6 and ∠7 = ∠8.
(i) ∠LAB + ∠BAM = 180° (As LAM is a straight line)
(∠LAB + ∠BAM) = x 180°
∠2 + ∠3 = 90° [Since, AC and AD are bisector of ∠LAB and ∠BAM]
∠CAD = 90°
∠A = 90°.
∠PBA + ∠QBA = 180° (As PBQ is a straight line)
(∠PBA + ∠QBA) = x 180°
∠6 + ∠7 = 90° [Since, BC and BD are bisector of ∠PBA and ∠QBA]
∠CBD = 90°
∠B = 90°.
∠LAB + ∠ABP = 180° (LM || PQ, sum of co-interior angles is 180°)
(∠LAB + ∠ABP) = x 180°
∠2 + ∠6 = 90° [Since, AC and BC are bisector of ∠LAB and ∠PBA]
In △ABC,
⇒ ∠2 + ∠6 + ∠C = 180°
⇒ 90° + ∠C = 180°
⇒ ∠C = 90°.
∠MAB + ∠ABQ = 180° (LM || PQ, sum of co-interior angles is 180°)
(∠MAB + ∠ABQ) = x 180°
∠3 + ∠7 = 90° [Since, AD and BD are bisector of ∠MAB and ∠ABQ]
In △ABD,
⇒ ∠3 + ∠7 + ∠D = 180°
⇒ 90° + ∠D = 180°
⇒ ∠D = 90°.
From figure,
∠BAM = ∠ABP (Alternate angles are equal)
∠3 = ∠6
∠LAB = ∠ABQ (Alternate angles are equal)
∠2 = ∠7
In △ABC and △ABD,
∠3 = ∠6 (Proved above)
∠2 = ∠7 (Proved above)
AB = AB (Common)
Hence, △ABC ≅ △ABD by ASA axiom.
∴ AD = BC and AC = BD (By C.P.C.T.)
Since, ∠A = ∠B = ∠C = ∠D = 90° and AD = BC, AC = BD.
Hence, proved that ACBD is a rectangle.
(ii) In △OAD,
OA = OD (Diagonals of rectangle bisect each other)
∠3 = ∠9 (Angles opposite to equal side are equal)
Since, ∠3 = 4,
∠9 = ∠4
Since, ∠9 and ∠4 are alternate angles and since they are equal we can say that,
⇒ OD || LM
⇒ CD || LM
Since, LM || PQ and CD || LM
⇒ CD || PQ.
Hence, proved that CD is parallel to the original parallel lines.
Answered By
23 Likes
Related Questions
ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ, prove that AP and DQ are perpendicular to each other.
If P and Q are points of trisection of the diagonal BD of a parallelogram ABCD, prove that CQ || AP.
In parallelogram ABCD, the bisector of ∠A meets DC in E and AB = 2AD. Prove that
(i) BE bisects ∠B
(ii) ∠AEB = a right angle.
ABCD is a parallelogram, bisectors of angles A and B meet at E which lies on DC. Prove that AB = 2AD.