Mathematics
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Answer
Let ABCD be a cyclic quadrilateral where diagonal AC and BD are diameters.
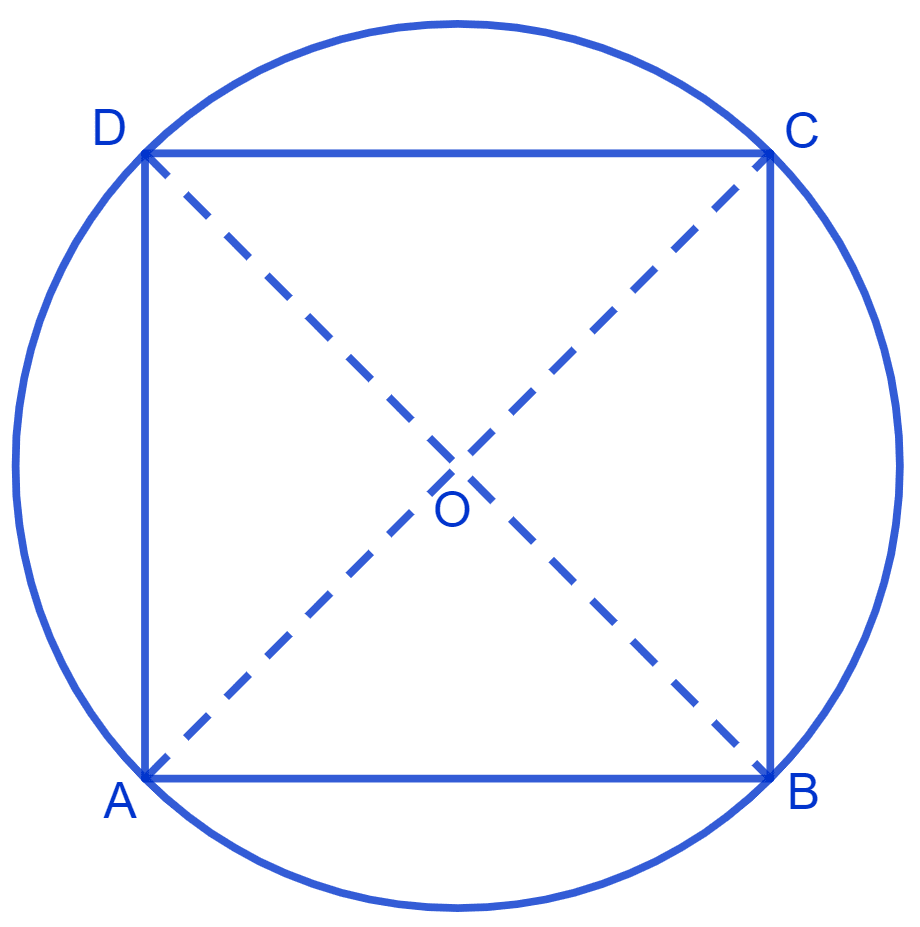
Since BD is a diameter.
Arc BAD is a semicircle, So ∠BAD = 90° (Angle in a semi circle is a right angle)
Since AC ia a diameter.
Arc ABC is a semicircle, So ∠ABC = 90° (Angle in a semi circle is a right angle)
Also,
ABCD is a cyclic quadrilateral
From figure,
⇒ ∠BCD + ∠BAD = 180° (Sum of opposite angles of cyclic quadrilateral is 180°)
⇒ ∠BCD + 90° = 180°
⇒ ∠BCD = 180° - 90°
⇒ ∠BCD = 90°.
⇒ ∠ABC + ∠ADC =180° (Sum of opposite angles of cyclic quadrilateral is 180°)
⇒ ∠ADC + 90° = 180°
⇒ ∠ADC = 180° - 90°
⇒ ∠ADC = 90°.
So, in quadrilateral ABCD
∠A = ∠B = ∠C = ∠D = 90°
Since, all angles equal to 90°.
Hence, proved that ABCD is a rectangle.
Related Questions
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
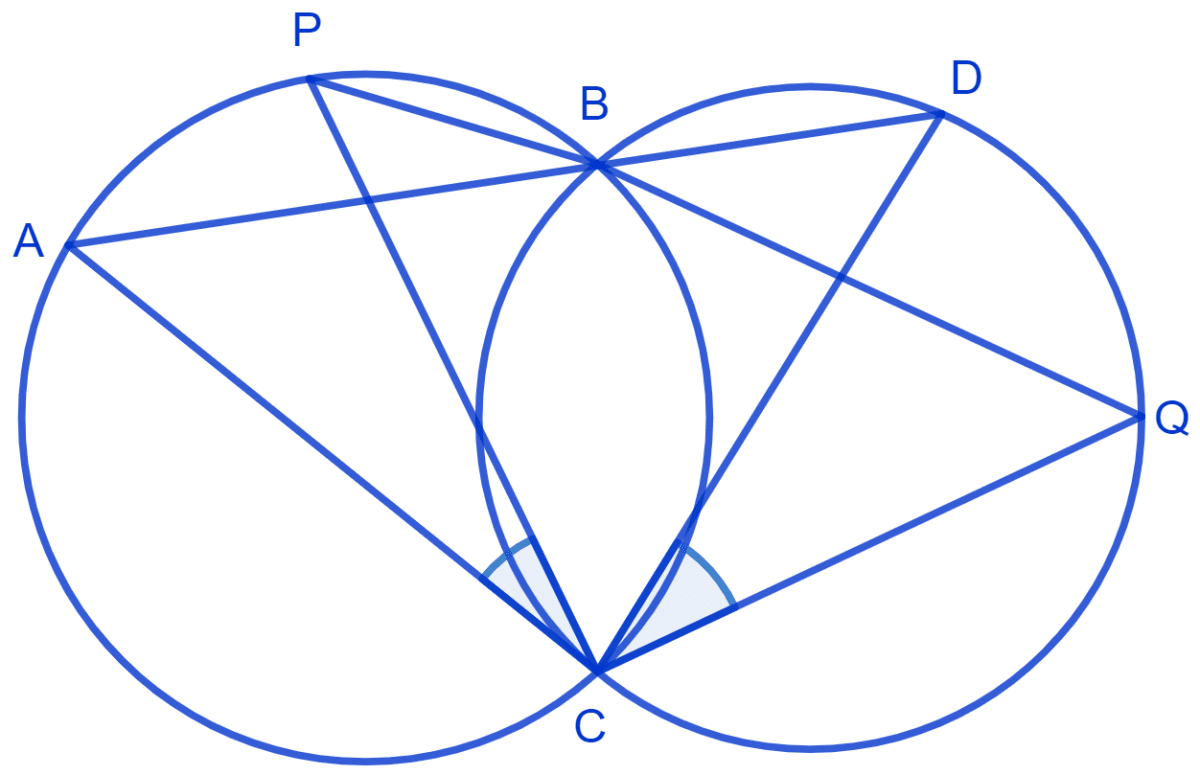
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively. Prove that ∠ACP = ∠QCD.
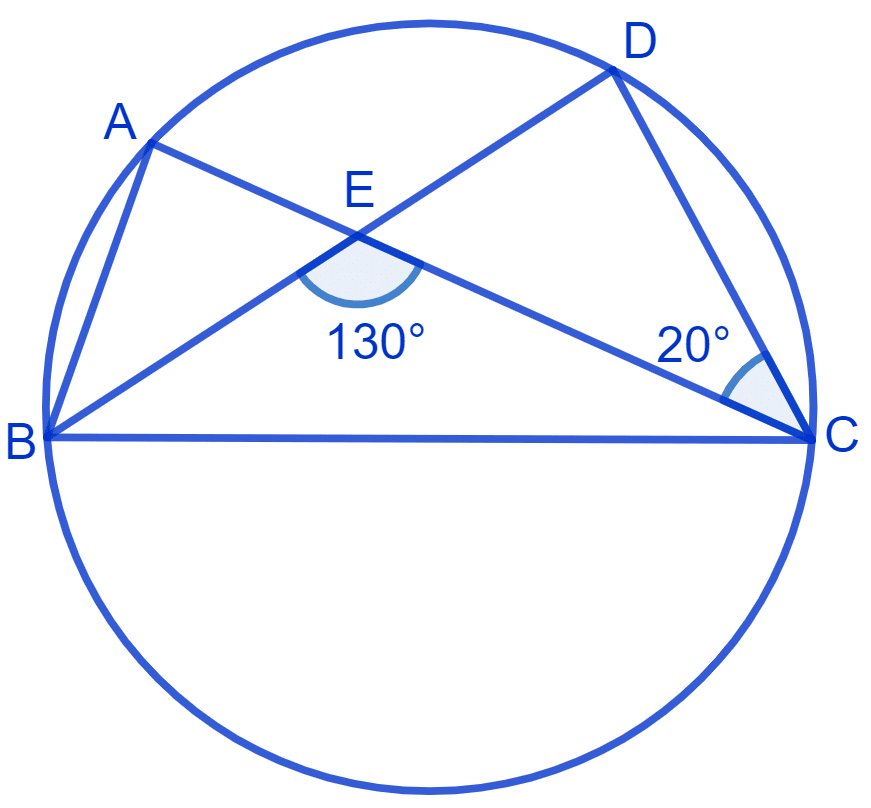
In Fig. A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.