If a, b, c are the sides of a right angled triangle where c is the hypotenuse, prove that the radius r of the circle which touches the sides of the triangle is given by r = $\dfrac{a + b - c}{2}$.

Let the circle touch the sides BC, CA and AB of the right triangle ABC at points D, E and F respectively,

where BC = a, CA = b and AB = c (as shown in the given figure).

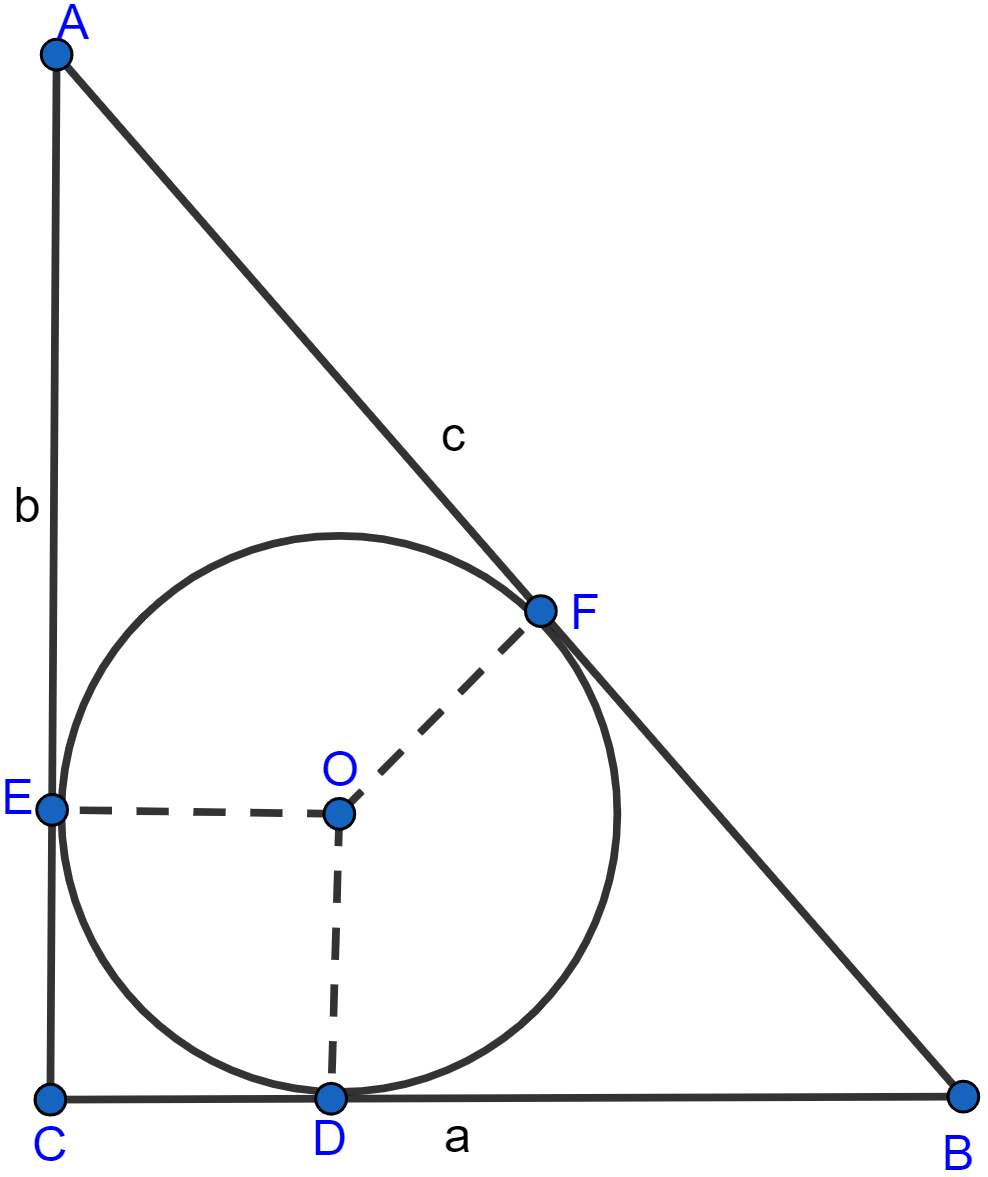
As the lengths of tangents drawn from an external point to a circle are equal

AE = AF, BD = BF and CD = CE

OD ⊥ BC and OE ⊥ CA (∵ tangents is ⊥ to radius)

ODCE is a square of side r

DC = CE = r

AF = AE = AC - EC = b - r and,

BF = BD = BC - DC = a - r

Now,

AB = AF + BF

⇒ c = (b - r) + (a - r)
⇒ c = b + a - 2r
⇒ 2r = a + b - c
⇒ r = $\dfrac{a + b - c}{2}$.

Hence, proved that r = $\dfrac{a + b - c}{2}$