(i) Define Electric Power and write its SI unit.

(ii) Two bulbs rated 100 W; 220 V and 60 W; 220 V are connected in parallel to an electric mains of 220 V. Find the current drawn by the bulbs from the mains.

(i) Electric power is the rate at which electric energy is dissipated or consumed in an electric circuit.

The SI unit of electric power is watt (W).

(ii) Given,

Voltage across the circuit = 220 V

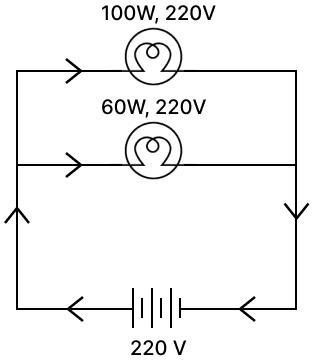
Power of first bulb (B₁) be (P₁) = 100 W

Power of second bulb (B₂) be P₂ = 60 W

P = $\dfrac{\text{V}^2}{\text{R}}$

or

R = $\dfrac{\text{V}^2}{\text{P}}$

Resistance across B₁ :

Substituting in formula we get,

R₁ = $\dfrac{\text{220}^2}{100}$ = 484 Ω

I = $\dfrac{\text{V}}{\text{R}}$

Substituting in formula we get,

I₁ = $\dfrac{220 }{484}$ = 0.454 A

Resistance across B₂ :

Substituting in formula above we get,

R₂ = $\dfrac{\text{220}^2}{60}$ = 806.6 Ω

and

I₂ = $\dfrac{220}{806.6}$ = 0.272 A

Now as they are connected in parallel, so the equivalent resistance is given by,

$\dfrac{1}{R$p} = \dfrac{1}{R1 + R2 } = \dfrac{1}{484} + \dfrac{1}{806.6} \\[1em] \Rightarrow \dfrac{1}{Rp} = \dfrac{806.6 + 484}{484 \times 806.6} \\[1em] \Rightarrow \dfrac{1}{Rp} = \dfrac{1290.6}{390394.4} \\[1em] \Rightarrow \dfrac{1}{Rp} = \dfrac{1}{5} \\[1em] \Rightarrow R_p = \dfrac{390394.4}{1290.6} = 302.5 Ω

So, equivalent resistance = 302.5 Ω

And current through mains is

I = $\dfrac{220}{302.5}$ = 0.727 A

Hence, current drawn by the bulbs from the mains = 0.727 A