Mathematics
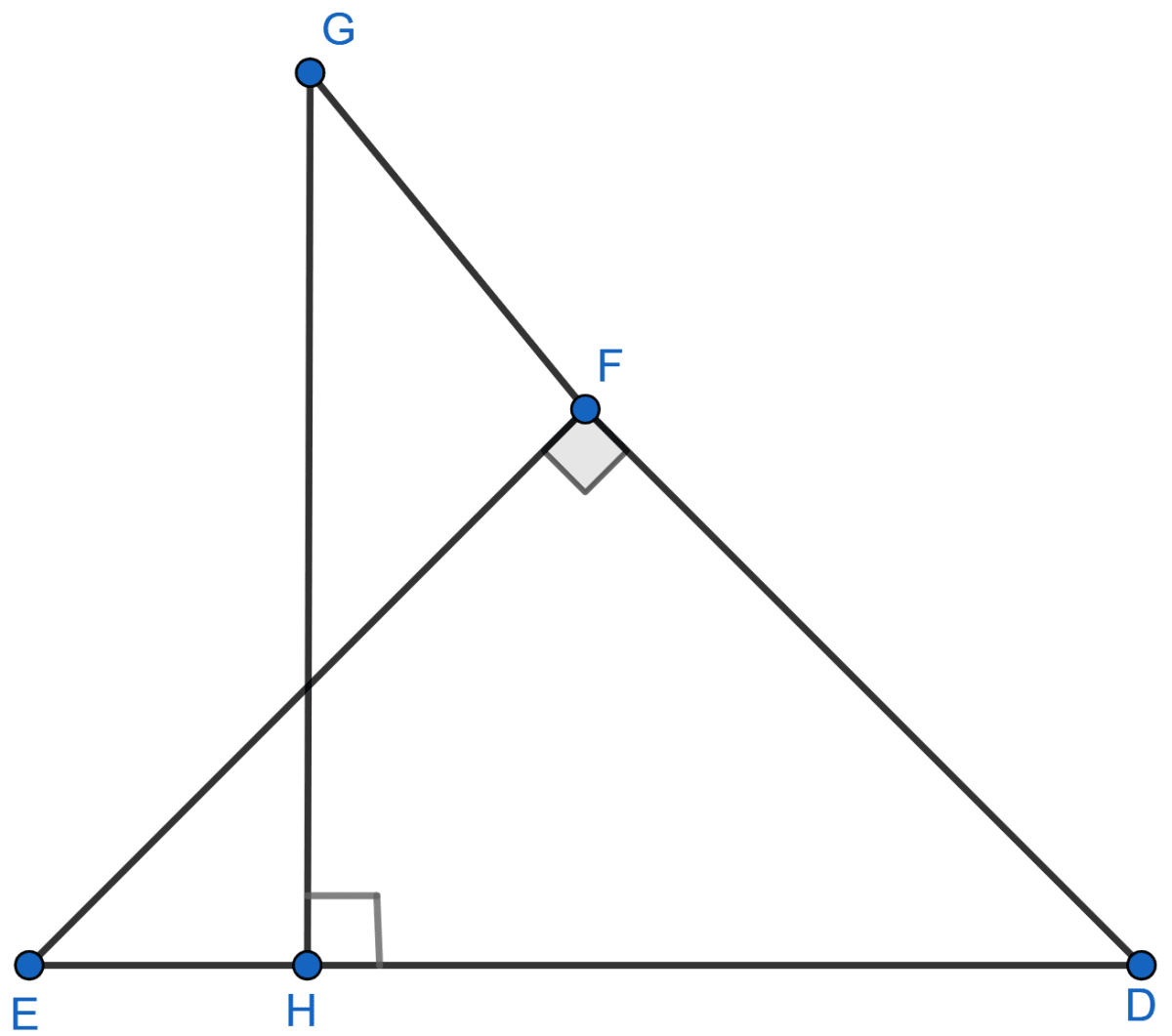
Given: ∠GHE = ∠DFE = 90°, DH = 8, DF = 12, DG = 3x – 1 and DE = 4x + 2.
Find: the lengths of segments DG and DE.
Similarity
Answer
In ΔDHG and ΔDFE,
⇒ ∠GHD = ∠DFE = 90°
⇒ ∠D = ∠D [Common]
Thus, ∆DHG ~ ∆DFE [By AA]
Since, corresponding sides of similar triangles are proportional we have :
DG = 3x - 1 = 3(7) - 1 = 21 - 1 = 20,
DE = 4x + 2 = 4(7) + 2 = 28 + 2 = 30.
Hence, DG = 20 and DE = 30.
Answered By
Related Questions
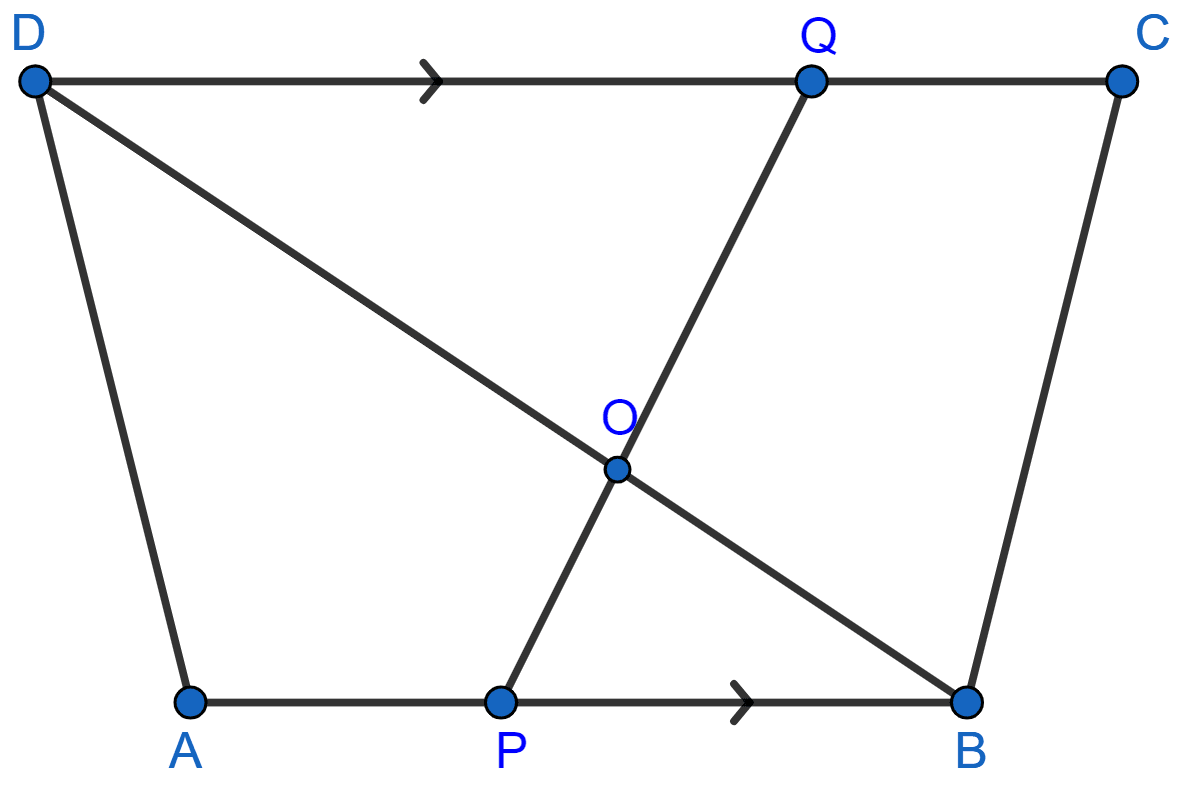
In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP x DO.
State, true or false:
(i) Two similar polygons are necessarily congruent.
(ii) Two congruent polygons are necessarily similar.
(iii) All equiangular triangles are similar.
(iv) All isosceles triangles are similar.
(v) Two isosceles-right triangles are similar.
(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
(vii) The diagonals of a trapezium, divide each other into proportional segments.
D is a point on the side BC of triangle ABC such that angle ADC is equal to angle BAC. Prove that: CA2 = CB x CD.
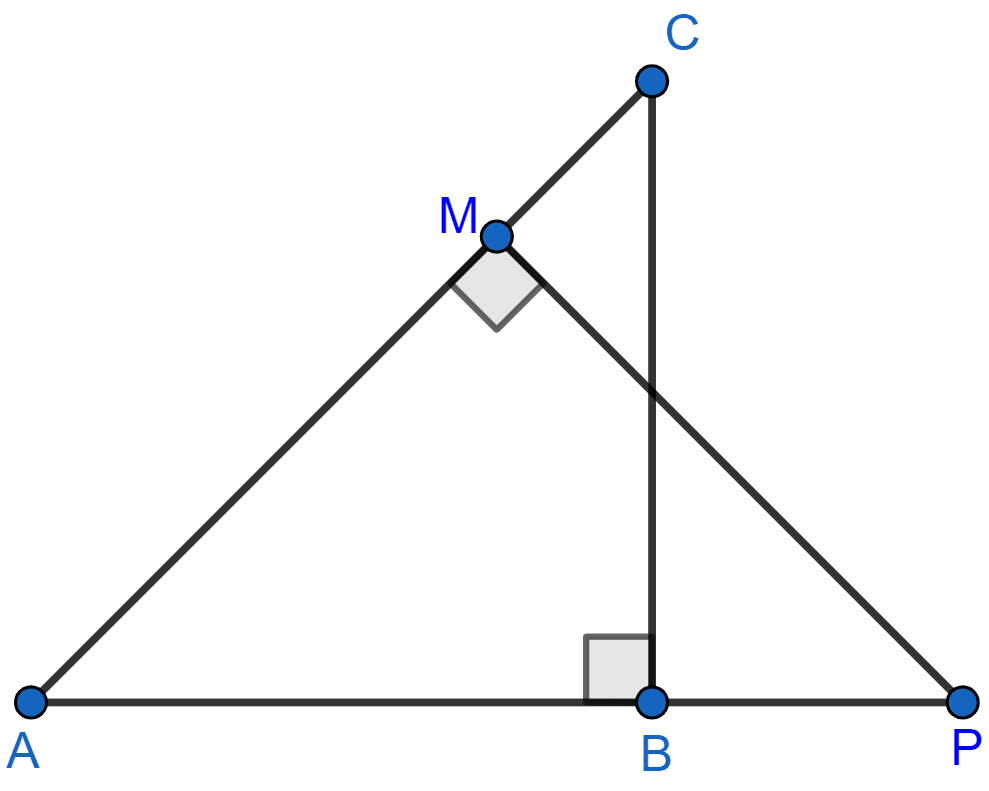
In the given figure, ΔABC and ΔAMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
(i) Prove that : ∆ABC ~ ∆AMP.
(ii) Find AB and BC.