Mathematics
Given : AB || DE and BC || EF. Prove that :
(i)
(ii) △DFG ~ △ACG.

Similarity
13 Likes
Answer
(i) In △ABG, DE || AB.
So, by basic proportionality theorem we get,
…..(1)
In △BCG, EF || BC.
So, by basic proportionality theorem we get,
…..(2)
From (1) and (2) we get,
Hence, proved that
(ii) In △DFG and △ACG,
⇒ [Proved above]
⇒ ∠DGF = ∠AGC [Common angle]
∴ △DFG ~ △ACG [By SAS]
Hence, proved that △DFG ~ △ACG.
Answered By
7 Likes
Related Questions
In the given figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that △ABC ~ △EBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of △BED = 9 cm2. Calculate the :
(i) length of AB
(ii) area of △ABC

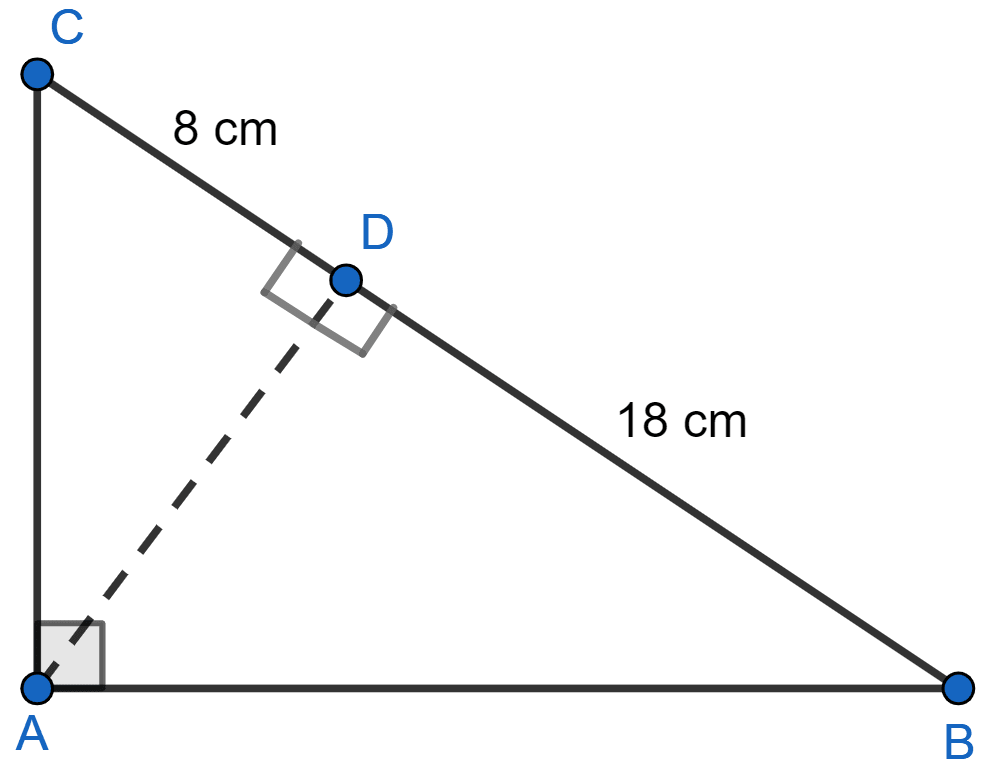
In the given figure, ABC is a right angled triangle with ∠BAC = 90°.
(i) Prove that : △ADB ~ △CDA.
(ii) If BD = 18 cm and CD = 8 cm, find AD.
(iii) Find the ratio of the area of △ADB is to area of △CDA.
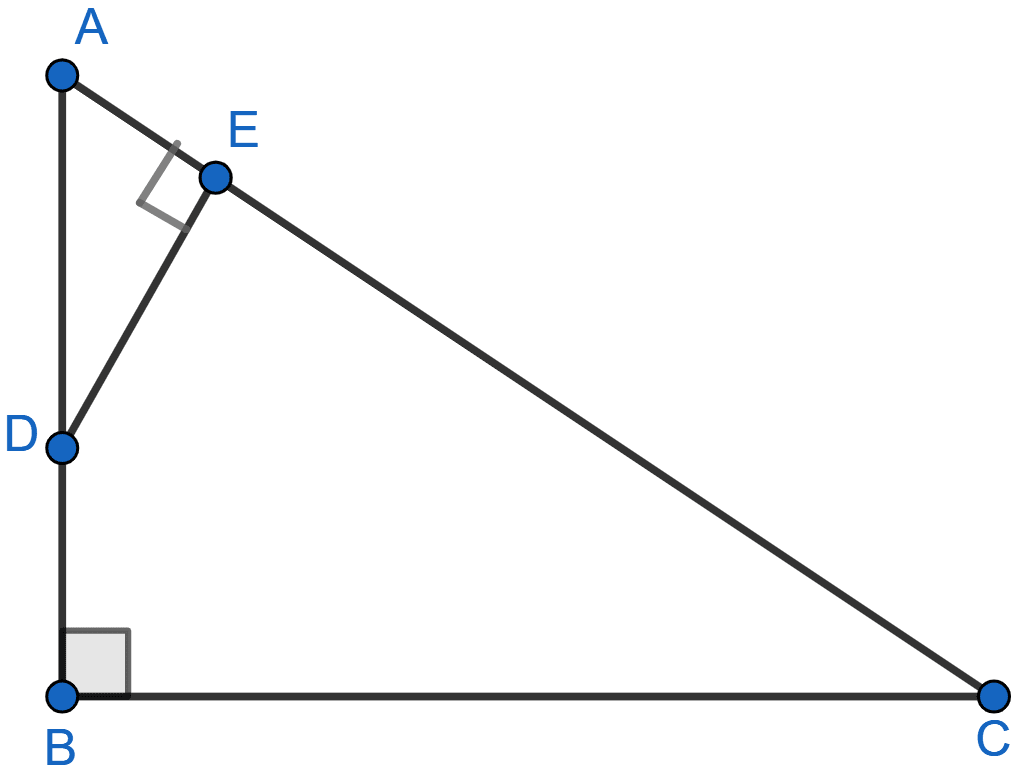
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
(i) △ADE ~ △ACB
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
(iii) Find, area of △ADE : area of quadrilateral BCED.
PQR is a triangle. S is a point on the side QR of △PQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
(i) Prove △PQR ~ △SPR.
(ii) Find the lengths of QR and PS.
(iii)
