KnowledgeBoat Logo

Mathematics

Given a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.

Section Formula

9 Likes

Answer

Let co-ordinates of A be (x, y) and D be (p, q).

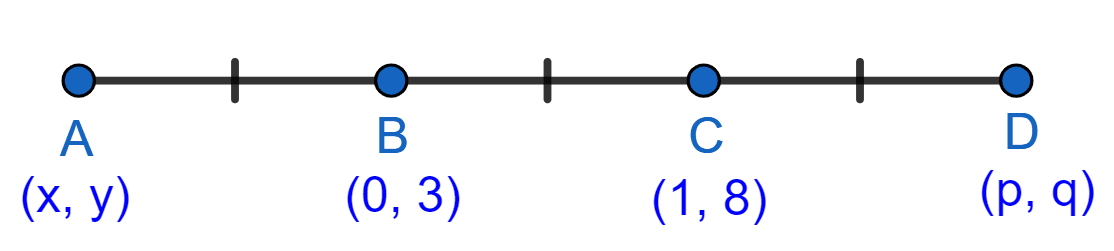
Given a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D. Section and Mid-Point Formula, Concise Mathematics Solutions ICSE Class 10.

Since, AB = BC.

B is the mid-point of AC.

By formula,

Mid-point = (x1+x22,y1+y22)\Big(\dfrac{x1 + x2}{2}, \dfrac{y1 + y2}{2}\Big)

Substituting values we get,

⇒B=(x+12,y+82)⇒(0,3)=(x+12,y+82)⇒0=x+12 and 3=y+82⇒x+1=0 and y+8=6⇒x=−1 and y=−2.\Rightarrow B = \Big(\dfrac{x + 1}{2}, \dfrac{y + 8}{2}\Big) \\[1em] \Rightarrow (0, 3) = \Big(\dfrac{x + 1}{2}, \dfrac{y + 8}{2}\Big) \\[1em] \Rightarrow 0 = \dfrac{x + 1}{2} \text{ and } 3 = \dfrac{y + 8}{2} \\[1em] \Rightarrow x + 1 = 0 \text{ and } y + 8 = 6 \\[1em] \Rightarrow x = -1 \text{ and } y = -2.

A = (x, y) = (-1, -2).

Since, BC = CD.

C is mid-point of BD.

By formula,

Mid-point = (x1+x22,y1+y22)\Big(\dfrac{x1 + x2}{2}, \dfrac{y1 + y2}{2}\Big)

Substituting values we get,

⇒C=(0+p2,3+q2)⇒(1,8)=(p2,3+q2)⇒1=p2 and 8=3+q2⇒p=2 and 3+q=16⇒p=2 and q=13.\Rightarrow C = \Big(\dfrac{0 + p}{2}, \dfrac{3 + q}{2}\Big) \\[1em] \Rightarrow (1, 8) = \Big(\dfrac{p}{2}, \dfrac{3 + q}{2}\Big) \\[1em] \Rightarrow 1 = \dfrac{p}{2} \text{ and } 8 = \dfrac{3 + q}{2} \\[1em] \Rightarrow p = 2 \text{ and } 3 + q = 16 \\[1em] \Rightarrow p = 2 \text{ and } q = 13.

D = (p, q) = (2, 13).

Hence, the co-ordinates of A = (-1, -2) and D = (2, 13).

Answered By

8 Likes

Related Questions