From the top of a light house 100 m high, the angles of depression of two ships are observed as 48° and 36° respectively. Find the distance between the two ships (in the nearest metre) if:

(i) the ships are on the same side of the light house.

(ii) the ships are on the opposite sides of the light house.

(i) Let's consider AB to be the lighthouse.

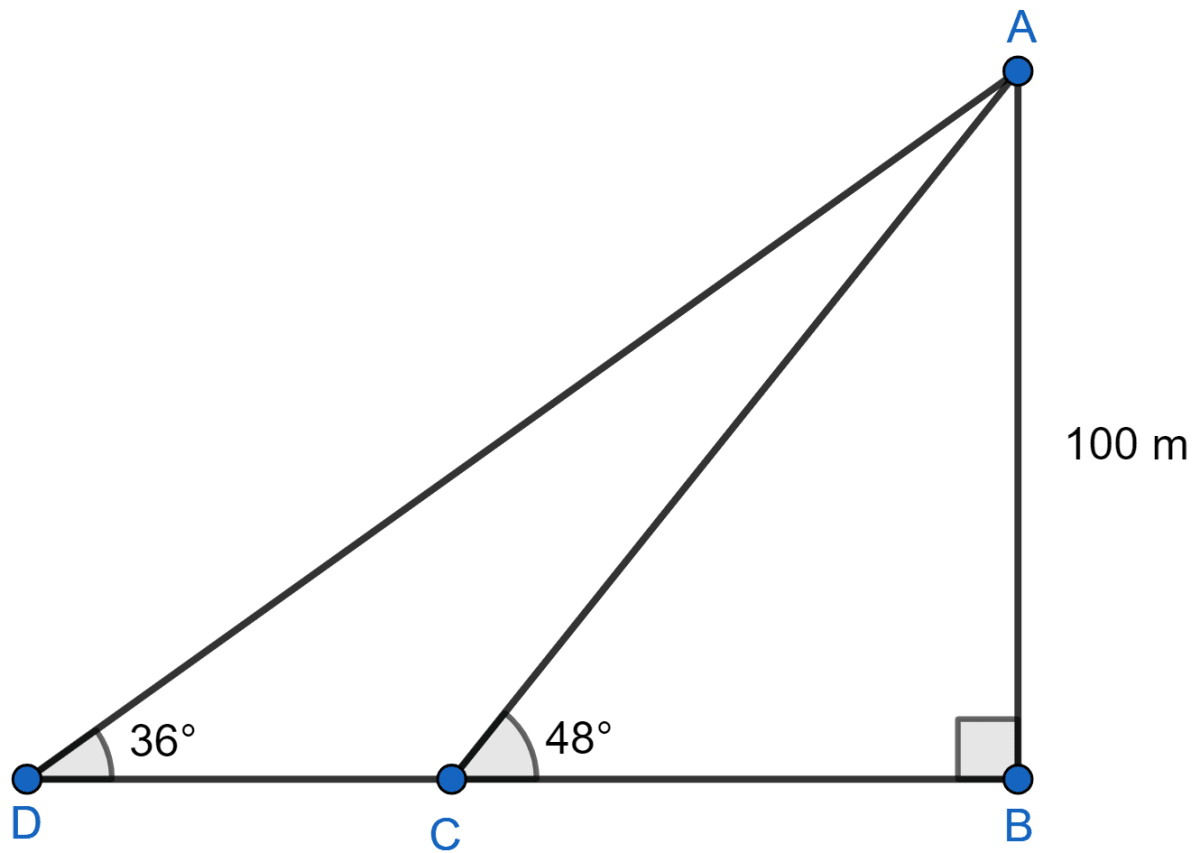
Given, depression angles are 48° and 36°.

When ships are on the same side,

In ∆ABC,

$\text{tan 48°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow 1.1106 = \dfrac{AB}{BC} \\[1em] \Rightarrow 1.1106 = \dfrac{100}{BC} \\[1em] \Rightarrow BC = \dfrac{100}{1.1106} \\[1em] \Rightarrow BC = 90.04 \text{ meters}.$

In ∆ABD,

$\text{tan 36°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow 0.7265 = \dfrac{AB}{BD} \\[1em] \Rightarrow 0.7265 = \dfrac{100}{BD} \\[1em] \Rightarrow BD = \dfrac{100}{0.7265} \\[1em] \Rightarrow BD = 137.64 \text{ meters}.$

Distance between the two ships (CD) = BD – BC = 137.64 - 90.04

= 47.6 ≈ 48 m.

Hence, distance between ships when on the same side = 48 m.

(ii) Let's consider AB to be the lighthouse.

Given, depression angles are 48° and 36°.

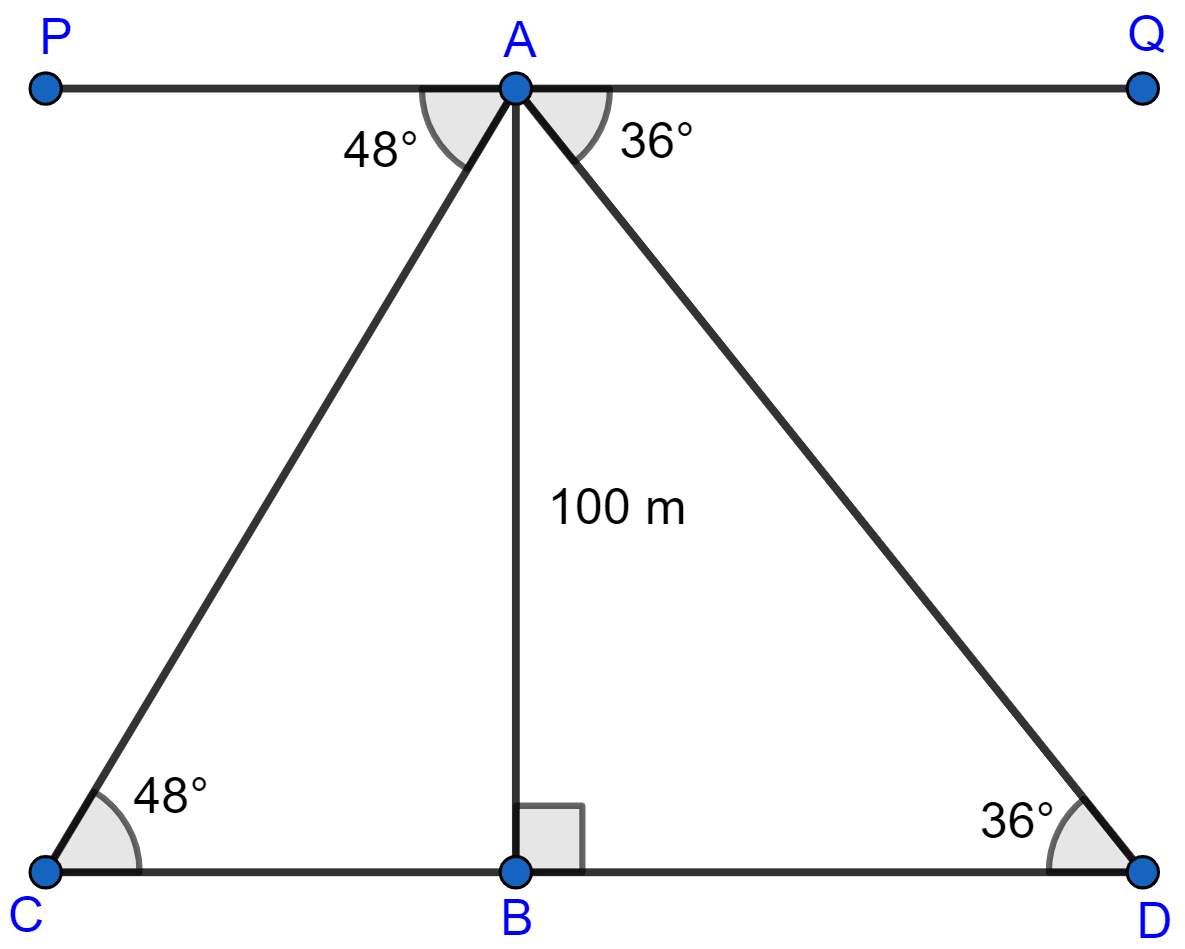
As, alternate angles are equal.

∴ ∠ADB = ∠QAD = 36° and ∠ACB = ∠PAC = 48°.

When ships are on the opposite side,

In ∆ABC,

$\text{tan 48°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow 1.1106 = \dfrac{AB}{BC} \\[1em] \Rightarrow 1.1106 = \dfrac{100}{BC} \\[1em] \Rightarrow BC = \dfrac{100}{1.1106} \\[1em] \Rightarrow BC = 90.04 \text{ meters}.$

In ∆ABD,

$\text{tan 36°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow 0.7265 = \dfrac{AB}{BD} \\[1em] \Rightarrow 0.7265 = \dfrac{100}{BD} \\[1em] \Rightarrow BD = \dfrac{100}{0.7265} \\[1em] \Rightarrow BD = 137.64 \text{ meters}.$

Distance between the two ships (CD) = BD + BC = 137.64 + 90.04

= 227.68 ≈ 228 m.

Hence, the distance between two ships, when on opposite side = 228 m.