Mathematics
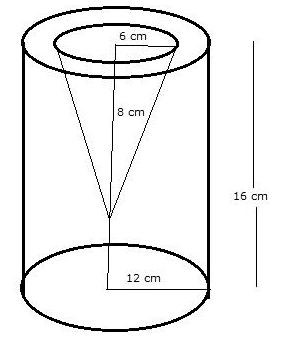
From a solid cylinder whose height is 16 cm and radius is 12 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out. Find the volume and total surface area of the remaining solid.
Mensuration
3 Likes
Answer
Given,
Height of the cylinder (H) = 16 cm
Radius of the base of cylinder (R) = 12 cm
Height of the cone (h) = 8 cm
Radius of the base of cone (r) = 6 cm
(i) Volume of remaining part (V) = Volume of cylinder - Volume of cone
Hence, volume of remaining part = 6939.43 cm3.
(ii) By formula,
⇒ l2 = r2 + h2
⇒ l2 = 62 + 82
⇒ l2 = 36 + 64
⇒ l2 = 100
⇒ l2 = 102
⇒ l = 10 cm.
Thus,
Total surface area of remaining solid (T) = Curved surface area of cylinder + Curved surface area of cone + Base area of cylinder + Area of circular ring on upper side of cylinder
(T) = 2πRH + πrl + πR2 + π(R2 - r2)
Hence, total surface area of remaining solid = 2187.43 cm2.
Answered By
2 Likes
Related Questions
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 80 m, calculate the total area of canvas required. Also, find the total cost of canvas used at ₹ 15 per meter if the width is 1.5 m.
The radius of a solid cylinder is doubled keeping the height same. The percentage increase in its volume is :
200%
100%
400%
300%
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and same base are removed. Find the volume of the remaining solid.
A circus tent is cylindrical to a height of 8 m surmounted by a conical part. If total height of the tent is 13 m and the diameter of its base is 24 m; calculate:
(i) total surface area of the tent
(ii) area of canvas, required to make this tent allowing 10% of the canvas used for folds and stitching.