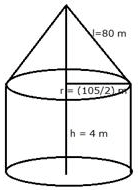
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 80 m, calculate the total area of canvas required. Also, find the total cost of canvas used at ₹ 15 per meter if the width is 1.5 m.

Given,

Radius of the cylindrical part of the tent (R) = $\dfrac{105}{2}$ m

Radius of conical part (r) = $\dfrac{105}{2}$ m.

Slant height (l) = 80 m

So, the total curved surface area of the tent = 2πRh + πrl

$= (2 \times \dfrac{22}{7} \times \dfrac{105}{2} \times 4) + (\dfrac{22}{7} \times \dfrac{105}{2} \times 80) \\[1em] = \dfrac{18480}{14} + \dfrac{184800}{14} \\[1em] = 1320 + 13200 \\[1em] = 14520 \text{ m}^2.$

Width of canvas used = 1.5 m

Length of canvas = $\dfrac{\text{Area of canvas}}{\text{Width of canvas}} = \dfrac{14520}{1.5} = 9680 \text{ m}$

Hence,

Total cost of canvas at the rate of ₹ 15 per meter = 9680 x 15 = ₹ 145200.

Hence, total area of canvas required = 9680 m² and cost = ₹ 145200.