Mathematics
From a deck of 52 cards, all the face cards are removed and then the remaining cards are shuffled. Now one card is drawn from the remaining deck. Find the probability that the card drawn is :
(i) a black card
(ii) 8 of red colour
(iii) a king of black colour.
Probability
2 Likes
Answer
There are 12 face cards in a deck.
Remaining cards = 40 (52 - 12)
No. of possible outcomes = 40.
(i) There are 26 black cards in a deck.
Since, face cards are removed and there are 6 black face cards (a king, queen and jack of both club and spades).
No. of black cards left = 26 - 6 = 20.
∴ No. of favourable outcomes = 20.
P(drawing a black card) = .
Hence, the probability of drawing a black card = .
(ii) There are 2 number 8 red cards (1 of each heart and diamond).
∴ No. of favourable outcomes = 2.
P(drawing a 8 of red colour) = .
Hence, the probability of drawing a 8 of red colour = .
(iii) There is no king left as all face cards are removed.
∴ No. of favourable outcomes = 0.
P(drawing a king of black colour) = = 0.
Hence, the probability of drawing a king of black colour = 0.
Answered By
1 Like
Related Questions
A game consists of spinning arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.
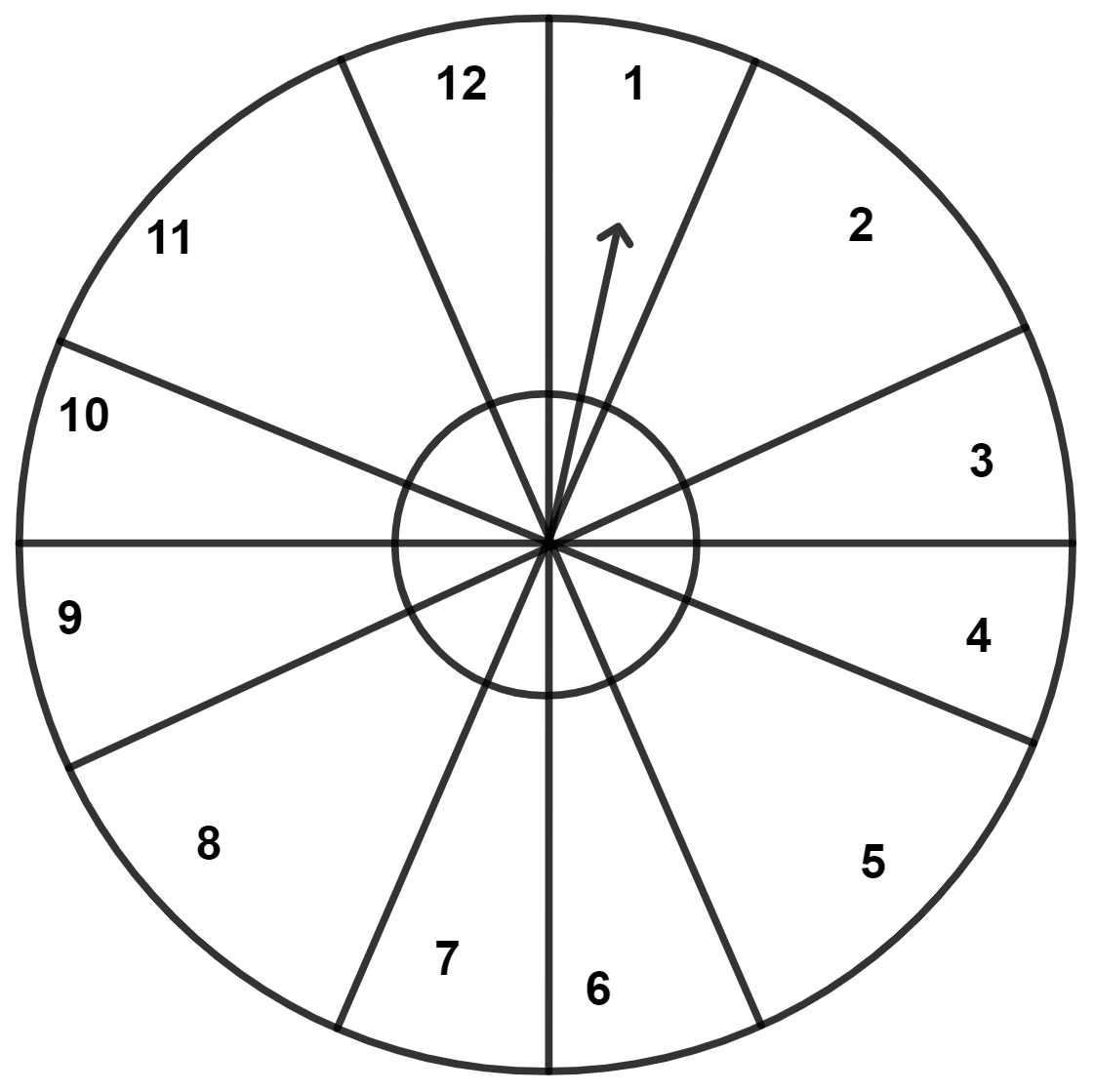
If the outcomes are equally likely, find the probability that the pointer will point at:
(i) 6
(ii) an even number
(iii) a prime number
(iv) a number greater than 8
(v) a number less than or equal to 9
(vi) a number between 3 and 11.
(i) 4 defective pens are accidentally mixed with 16 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is drawn at random from the lot. What is the probability that the pen is defective ?
(ii) Suppose the pen drawn in (i) is defective and is not replaced. Now one more pen is drawn at random from the rest. What is the probability that this pen is :
(a) defective ?
(b) not defective ?
One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting :
(i) a queen of red color
(ii) a black face card
(iii) the jack or the queen of the hearts
(iv) a diamond
(v) a diamond or a spade
Seven cards : the eight, the nine, the ten, jack, queen, king and ace of diamonds are well shuffled. One card is then picked up at random.
(i) What is the probability that the card drawn is the eight or the king ?
(ii) If the king is drawn and put aside, what is the probability that the second card picked up is :
(a) an ace ?
(b) a king ?