A game consists of spinning arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.

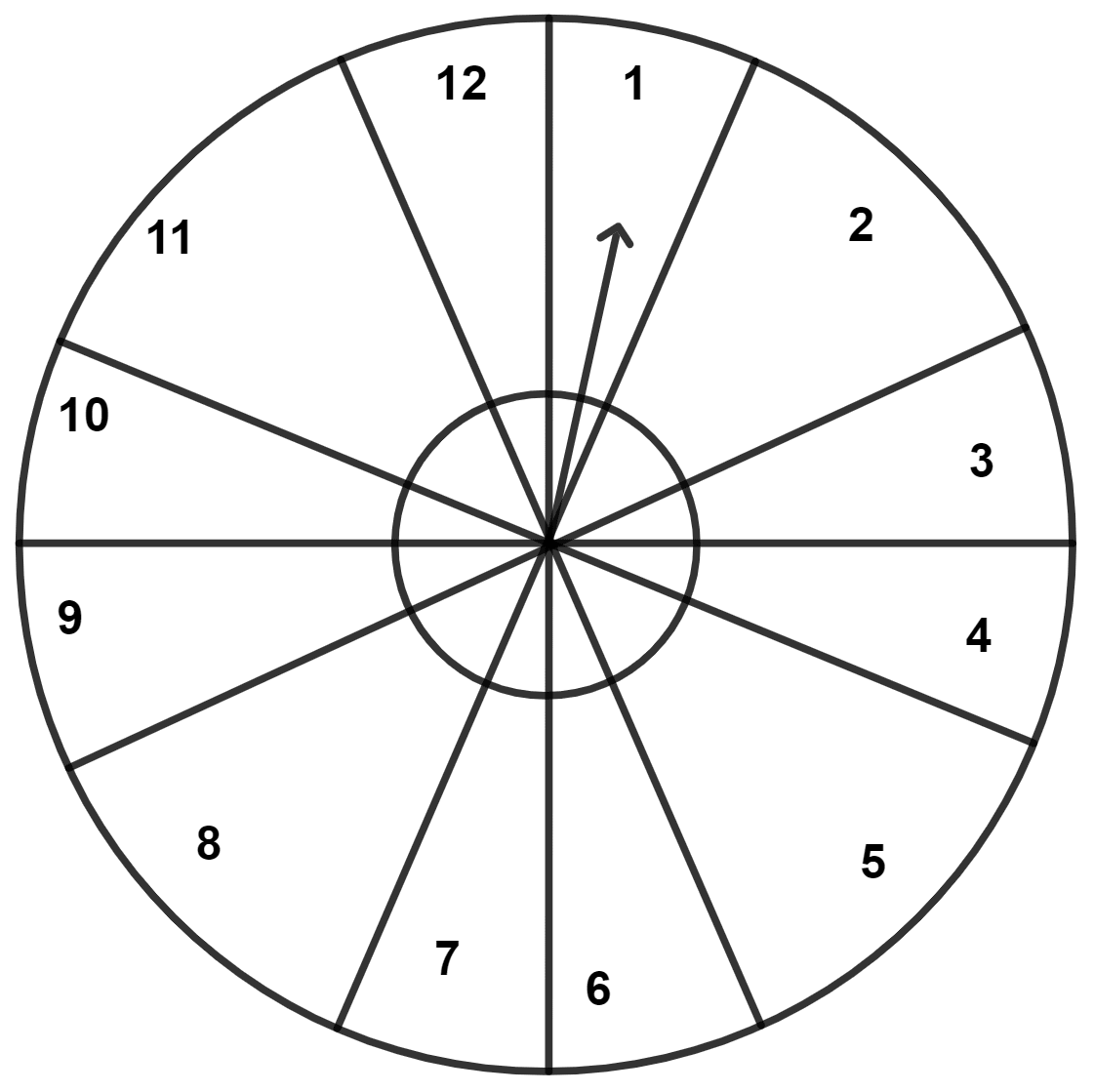
If the outcomes are equally likely, find the probability that the pointer will point at:

(i) 6

(ii) an even number

(iii) a prime number

(iv) a number greater than 8

(v) a number less than or equal to 9

(vi) a number between 3 and 11.

We have,

Total number of possible outcomes = 12

(i) Number of favorable outcomes for 6 = 1

P(that pointer points at 6) = $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{1}{12}$.

Hence, the probability that pointer points at 6 = $\dfrac{1}{12}$.

(ii) Favorable outcomes for an even number are 2, 4, 6, 8, 10, 12.

∴ Number of favorable outcomes = 6

P(that pointer points at an even number)

= $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{6}{12} = \dfrac{1}{2}$.

Hence, the probability that pointer points at an even number = $\dfrac{1}{2}$.

(iii) Favorable outcomes for a prime number are 2, 3, 5, 7, 11.

∴ Number of favorable outcomes = 5

P(that pointer points at a prime number)

= $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{5}{12}$.

Hence, the probability that pointer points at a prime number = $\dfrac{5}{12}$.

(iv) Favorable outcomes for a number greater than 8 are 9, 10, 11, 12.

∴ Number of favorable outcomes = 4.

P(that pointer points at a number greater than 8)

= $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{4}{12} = \dfrac{1}{3}$.

Hence, the probability that pointer points at a number greater than 8 = $\dfrac{1}{3}$.

(v) Favorable outcomes for a number less than or equal to 9 are 1, 2, 3, 4, 5, 6, 7, 8, 9

∴ Number of favorable outcomes = 9

P(that pointer points at a number less than or equal to 9)

= $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{9}{12} = \dfrac{3}{4}$.

Hence, the probability that pointer points at a number less than or equal to 9 = $\dfrac{3}{4}$.

(vi) Favorable outcomes for a number between 3 and 11 are 4, 5, 6, 7, 8, 9, 10

∴ Number of favorable outcomes = 7

P(that pointer points at a number between 3 and 11)

= $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{7}{12}$.

Hence, the probability that pointer points at a number between 3 and 11 = $\dfrac{7}{12}$.