Mathematics
Find the equation of the line that is perpendicular to 3x + 2y - 8 = 0 and passes through the mid-point of the line segment joining the points (5, -2) and (2, 2).
Straight Line Eq
41 Likes
Answer
Given equation of line,
⇒ 3x + 2y - 8 = 0
Converting it in the form y = mx + c,
⇒ 2y = -3x + 8
⇒ y =
Comparing with y = mx + c we get,
Slope (m1) =
Now, the coordinates of the mid-point of the line segment joining the points (5, -2) and (2, 2) will be
Let's consider the slope of the line perpendicular to the given line be m2.
Then,
The equation of the new line with slope m2 and passing through can be given by point-slope form i.e.,
y - y1 = m(x - x1)
Putting values we get,
Hence, the equation of the line is 2x - 3y - 7 = 0.
Answered By
19 Likes
Related Questions
(i) The line 4x - 3y + 12 = 0 meets the x-axis at A. Write down the coordinates of A.
(ii) Determine the equation of the line passing through A and perpendicular to 4x - 3y + 12 = 0.
Find the equation of the line that is parallel to 2x + 5y - 7 = 0 and passes through the mid-point of the line segment joining the points (2, 7) and (-4, 1).
Find the equation of a straight line passing through the intersection of 2x + 5y - 4 = 0 with x-axis and parallel to the line 3x - 7y + 8 = 0.
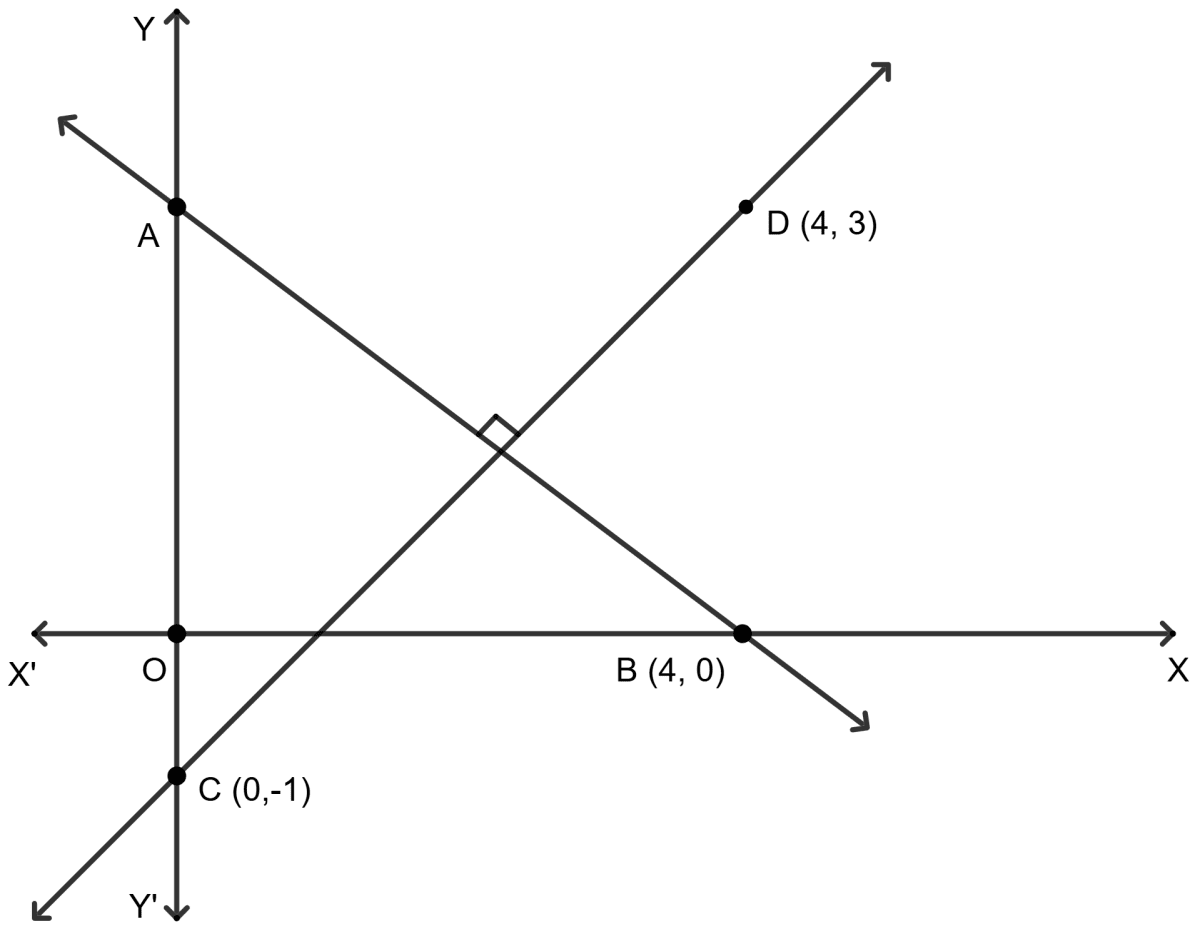
Line AB is perpendicular to line CD. Coordinates of B, C and D are (4, 0), (0, -1) and (4, 3) respectively. Find
(i) the slope of CD
(ii) the equation of line AB