Mathematics
Find the area of the quadrilateral field ABCD whose sides AB = 40 m, BC = 28 m, CD = 15 m, AD = 9 m and ∠A = 90°.
Mensuration
Answer
From figure,
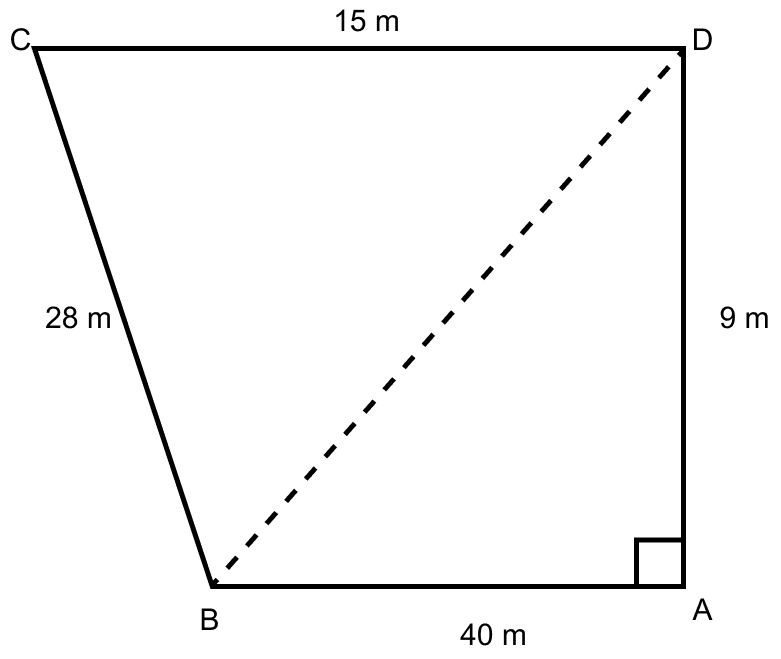
ABCD is a quadrilateral field.
In triangle BAD,
∠A = 90°
Using the Pythagoras Theorem
⇒ BD2 = AB2 + AD2
Substituting the values we get,
⇒ BD2 = 402 + 92
⇒ BD2 = 1600 + 81 = 1681
⇒ BD = = 41 m
We know that,
Area of quadrilateral ABCD = Area of △BAD + Area of △BDC
Calculating area of △BDC,
In △BDC,
Let a = BD = 41 m, b = BC = 28 m and c = CD = 15 m.
Semi-perimeter (s) = = 42 m.
By Heron's formula,
Area of triangle =
Substituting values we get,
Calculating area of △BAD,
Area of quadrilateral ABCD = Area of △BAD + Area of △BDC
= 180 + 126
= 306 m2.
Hence, area of quadrilateral ABCD = 306 m2.
Answered By
Related Questions
Find the area of quadrilateral whose one diagonal is 20 cm long and the perpendiculars to this diagonal from other vertices are of length 9 cm and 15 cm.
Find the area of a quadrilateral whose diagonals are of length 18 cm and 12 cm and they intersect each other at right angles.
Find the area of the quadrilateral ABCD in which ∠BCA = 90°, AB = 13 cm and ACD is an equilateral triangle of side 12 cm.
Find the area of quadrilateral ABCD in which ∠B = 90° , AB = 6 cm, BC = 8 cm and CD = AD = 13 cm.