Find the area of the quadrilateral field ABCD whose sides AB = 40 m, BC = 28 m, CD = 15 m, AD = 9 m and ∠A = 90°.

From figure,

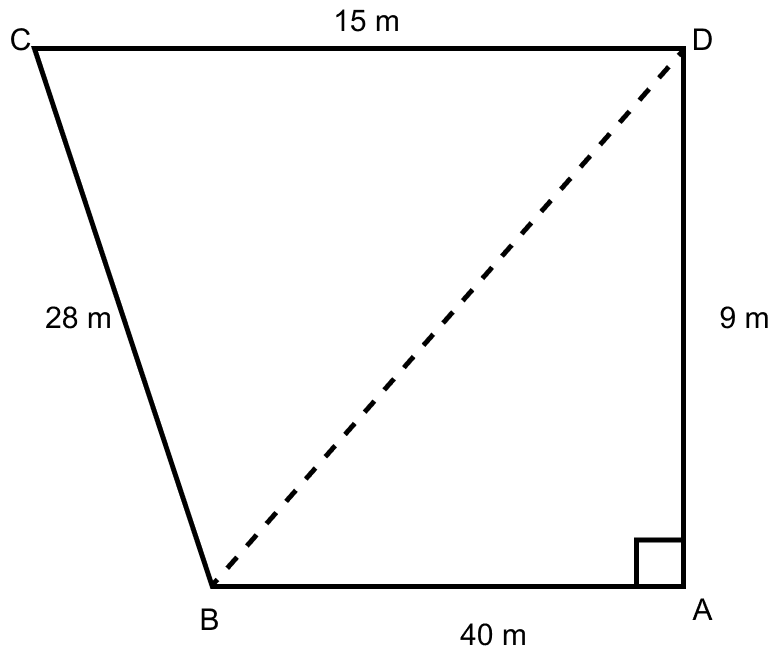
ABCD is a quadrilateral field.

In triangle BAD,

∠A = 90°

Using the Pythagoras Theorem

⇒ BD² = AB² + AD²

Substituting the values we get,

⇒ BD² = 40² + 9²

⇒ BD² = 1600 + 81 = 1681

⇒ BD = $\sqrt{1681}$ = 41 m

We know that,

Area of quadrilateral ABCD = Area of △BAD + Area of △BDC

Calculating area of △BDC,

In △BDC,

Let a = BD = 41 m, b = BC = 28 m and c = CD = 15 m.

Semi-perimeter (s) = $\dfrac{a + b + c}{2} = \dfrac{41 + 28 + 15}{2} = \dfrac{84}{2}$ = 42 m.

By Heron's formula,

Area of triangle = $\sqrt{s(s - a)(s - b)(s - c)}$

Substituting values we get,

$A = \sqrt{42(42 - 41)(42 - 28)(42 - 15)} \\[1em] = \sqrt{42 \times 1 \times 14 \times 27} \\[1em] = \sqrt{15876} \\[1em] = 126 \text{ m}^2.$

Calculating area of △BAD,

$\text{Area of △BAD } = \dfrac{1}{2} \times \text{ base × height} \\[1em] = \dfrac{1}{2} \times BA \times AD \\[1em] = \dfrac{1}{2} \times 40 \times 9 \\[1em] = 180 \text{ m}^2$

Area of quadrilateral ABCD = Area of △BAD + Area of △BDC

= 180 + 126

= 306 m².

Hence, area of quadrilateral ABCD = 306 m².