Mathematics
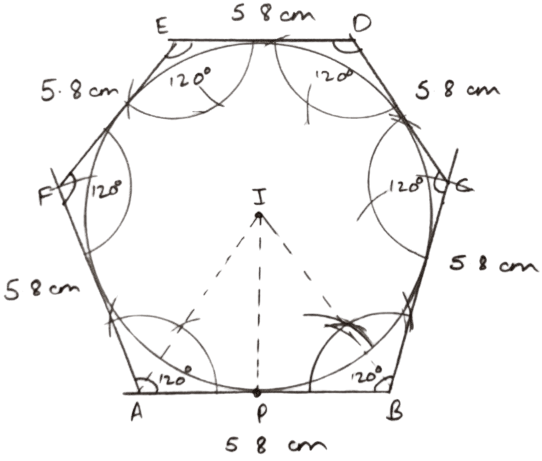
Draw an inscribing circle of regular hexagon of side 5.8 cm.
Constructions
16 Likes
Answer
Each interior angle of a regular hexagon =
Steps of construction :
Draw a regular hexagon ABCDEF with each side equal to 5.8 cm and each interior angle = 120°.
Draw the bisectors of interior angles at A and B which intersect each other at point I.
From point I , draw IP perpendicular to AB.
With I as center and IP as radius, draw a circle which will touch all the sides of the regular hexagon drawn.
Hence, above is the required incircle of regular hexagon.
Answered By
9 Likes
Related Questions
(i) Using ruler and compasses only, construct a triangle ABC in which AB = 8 cm, BC = 6 cm and CA = 5 cm.
(ii) Find its incenter and mark it I.
(iii) With I as centre, draw a circle which will cut off 2 cm chords from each side of the triangle.
Draw a circle circumscribing a regular hexagon with side = 5 cm.
Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm and ∠ABC = 120°.
(i) Construct a circle circumscribing the triangle ABC.
(ii) Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Using a ruler and compasses only :
(i) Construct a triangle ABC with the following data :
AB = 3.5 cm, BC = 6 cm and ∠ABC = 120°.
(ii) In same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
(iii) Measure ∠BCP.