Mathematics
Draw an angle ABC = 75°. Find a point P such that P is at a distance of 2 cm from AB and 1.5 cm from BC.
Locus
7 Likes
Answer
Steps of construction :
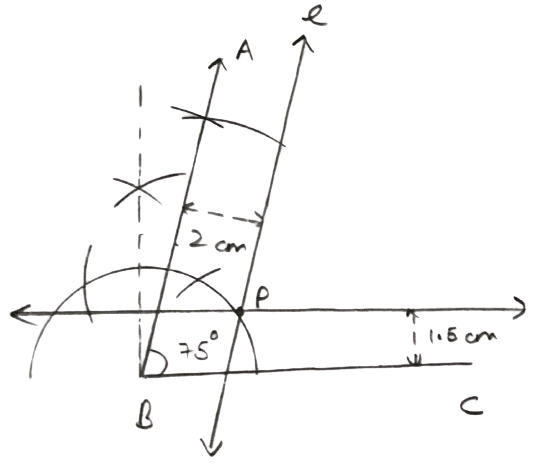
Draw a ray BC.
At B, draw a ray BA making an angle of 75° with BC.
Draw a line l parallel to AB at a distance of 2 cm.
Draw another line m parallel to BC at a distance of 1.5 cm which intersects line l at P.
Hence, P is the required point.
Answered By
3 Likes
Related Questions
Construct a triangle ABC, with AB = 6 cm, AC = BC = 9 cm. Find a point 4 cm from A and equidistant from B and C.
A straight line AB is 8 cm long. Draw and describe the locus of a point which is :
(i) always 4 cm from the line AB.
(ii) equidistant from A and B.
Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.
Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained.
Draw a triangle ABC in which AB = 6 cm, BC = 4.5 cm and AC = 5 cm. Draw and label :
(i) the locus of the centers of all circles which touch AB and AC,
(ii) the locus of the centers of all the circles of radius 2 cm which touch AB.
Hence, construct the circle of radius 2 cm which touches AB and AC.