Draw a triangle ABC in which AB = 6 cm, BC = 4.5 cm and AC = 5 cm. Draw and label :

(i) the locus of the centers of all circles which touch AB and AC,

(ii) the locus of the centers of all the circles of radius 2 cm which touch AB.

Hence, construct the circle of radius 2 cm which touches AB and AC.

Steps of construction :

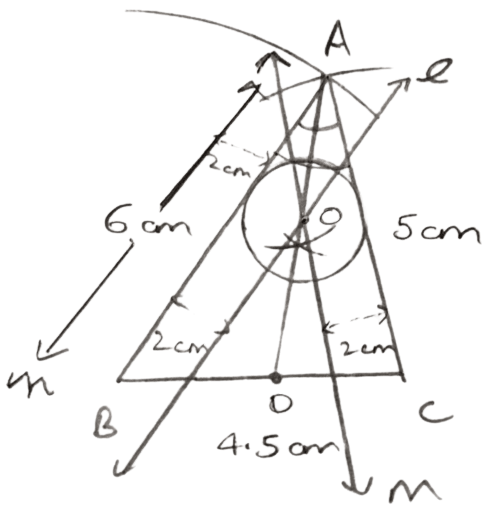
1. Draw a line segment BC = 4.5 cm

2. With B as center and radius = 6 cm and C as center and radius = 5 cm, draw arcs which intersect each other at A.

3. Join AB and AC. ABC is the required triangle.

4. Draw AD, the angle bisector of ∠BAC.

5. Draw lines l and n parallel to AB and m parallel to AC at a distance of 2 cm, which intersect each other and AD at O.

6. With center O and radius 2 cm, draw a circle which touches AB and AC.

(i) The locus of the centers of all circles which touch AB and AC is AD, the angle bisector of angle A.

(ii) The locus of the centers of all the circles of radius 2 cm which touch AB is line l and n.