Mathematics
Draw a circle of radius 5 cm. Draw two tangents to this circle so that the angle between tangents is 45°.
Answer
Steps of Construction :
Draw a circle with center O, radius = 5 cm and BC as diameter.
Draw arcs making an angle of 135° (180° - 45°) at O such that ∠AOB = 135°.
At A and B, draw two rays making an angle of 90° at each point which meet other at point P.
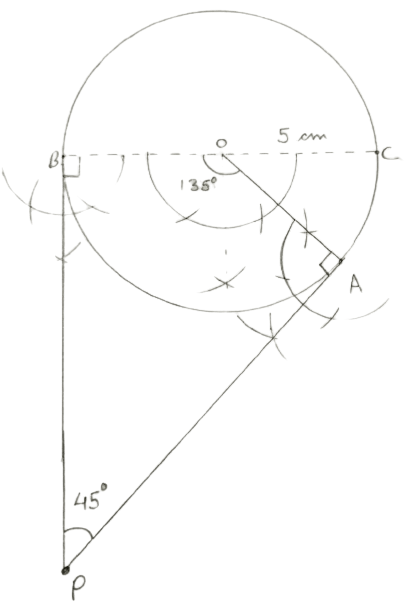
Hence, AP and BP are required tangents making an angle of 45° with each other.
Related Questions
Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.
Using ruler and compasses only,
(i) Construct triangle ABC, having given BC = 7 cm, AB - AC = 1 cm and ∠ABC = 45°.
(ii) Inscribe a circle in the △ABC constructed in (i) above.
ABC is an isosceles triangle with AB = AC. Circles are drawn with AB and AC as diameters. The two circles intersect each other at vertex A and a point P which lies in side BC, ∠APB is :
60°
75°
90°
120°
Draw a circle of radius 3 cm. Mark a point P at a distance of 5 cm from the center of the circle drawn. Draw two tangents PA and PB to the given circle and measure the length of each tangent.