Mathematics
Diagonals AC and BD of a parallelogram ABCD intersect at O. Given that AB = 12 cm and perpendicular distance between AB and DC is 6 cm. Calculate the area of the triangle AOD.
Mensuration
53 Likes
Answer
Let ABCD be a parallelogram with AC and BD the diagonals intersecting at O.
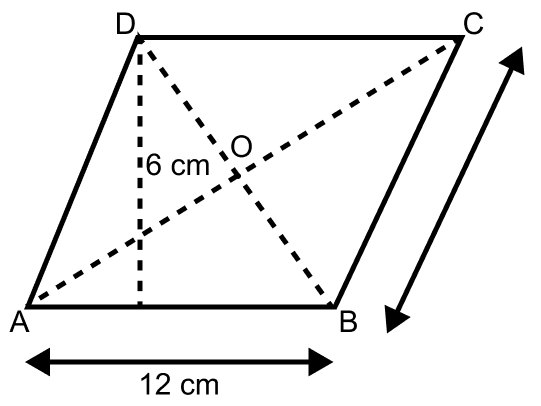
From figure,
AB = 12 cm and DM = 6 cm.
By formula,
Area of parallelogram ABCD = base × height = AB × DM
= 12 × 6
= 72 cm2.
Since, diagonals of parallelogram intersect each other so O is the mid-point of BD.
∴ AO is the median of the △ABD.
Since, median divides the triangle into two triangles of equal area,
∴ Area of △AOD = × Area of △ABD ……(1)
Since, diagonal of a parallelogram divides it into two triangles of equal area.
∴ Area of △ABD = × Area of || gm ABCD.
Substituting above value of △ABD in equation 1 we get,
Area of △AOD = Area of || gm ABCD
= = 18 cm2.
Hence, area of △AOD = 18 cm2.
Answered By
18 Likes
Related Questions
Two adjacent sides of a parallelogram are 15 cm and 10 cm. If the distance between the longer sides is 8 cm, find the area of the parallelogram. Also find the distance between shorter sides.
ABCD is a parallelogram with sides AB = 12 cm, BC = 10 cm and diagonal AC = 16 cm. Find the area of the parallelogram. Also find the distance between its shorter sides.
ABCD is a parallelogram with side AB = 10 cm. Its diagonals AC and BD are of length 12 cm and 16 cm respectively. Find the area of the parallelogram ABCD.
The area of a parallelogram is p cm2 and its height is q cm. A second parallelogram has equal area but its base is r cm more than that of the first. Obtain an expression in terms of p, q and r for the height h of the second parallelogram.