Mathematics
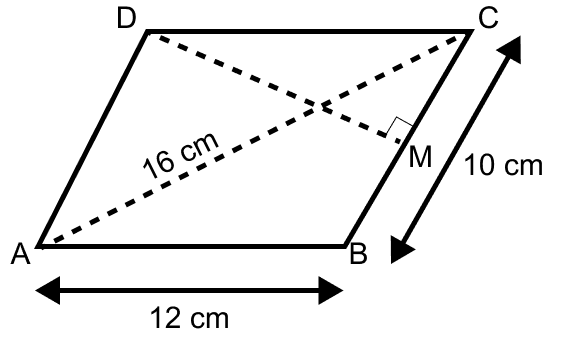
ABCD is a parallelogram with sides AB = 12 cm, BC = 10 cm and diagonal AC = 16 cm. Find the area of the parallelogram. Also find the distance between its shorter sides.
Mensuration
44 Likes
Answer
In triangle ABC,
Let,
BC = a = 10 cm, AC = b = 16 cm and AB = c = 12 cm.
We know that,
Semi-perimeter (s) =
= = 19 cm.
By Heron's formula,
We know that,
Diagonal of a parallelogram divides it into two triangles of equal area.
∴ Area of triangle ABC = Area of triangle ADC
∴ Area of parallelogram = 2 × Area of triangle ABC.
= 2 × 59.9
= 119.8 cm2.
Let DM be the distance between the shorter sides of the parallelogram.
By formula,
Area of parallelogram = base × height = BC × DM
Substituting the values we get,
⇒ 119.8 = 10 × DM
⇒ DM =
⇒ DM = 11.98 cm.
Hence, the distance between shorter sides = 11.98 cm and area of parallelogram = 119.8 cm2.
Answered By
8 Likes
Related Questions
A wire when bent in the form of an equilateral triangle encloses an area of cm2. Find the area enclosed by the same wire when bent to form:
(i) a square, and
(ii) a rectangle whose length is 2 cm more than its width.
Two adjacent sides of a parallelogram are 15 cm and 10 cm. If the distance between the longer sides is 8 cm, find the area of the parallelogram. Also find the distance between shorter sides.
Diagonals AC and BD of a parallelogram ABCD intersect at O. Given that AB = 12 cm and perpendicular distance between AB and DC is 6 cm. Calculate the area of the triangle AOD.
ABCD is a parallelogram with side AB = 10 cm. Its diagonals AC and BD are of length 12 cm and 16 cm respectively. Find the area of the parallelogram ABCD.