Mathematics
D is a point on the side BC of triangle ABC such that angle ADC is equal to angle BAC. Prove that: CA2 = CB x CD.
Similarity
6 Likes
Answer
In ΔADC and ΔBAC,

⇒ ∠ADC = ∠BAC [Given]
⇒ ∠ACD = ∠ACB [Common]
∴ ∆ADC ~ ∆BAC [By AA]
Since, corresponding sides of similar triangles are proportional we have :
⇒
⇒ CA2 = CB x CD.
Hence, proved that CA2 = CB x CD.
Answered By
5 Likes
Related Questions
State, true or false:
(i) Two similar polygons are necessarily congruent.
(ii) Two congruent polygons are necessarily similar.
(iii) All equiangular triangles are similar.
(iv) All isosceles triangles are similar.
(v) Two isosceles-right triangles are similar.
(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
(vii) The diagonals of a trapezium, divide each other into proportional segments.
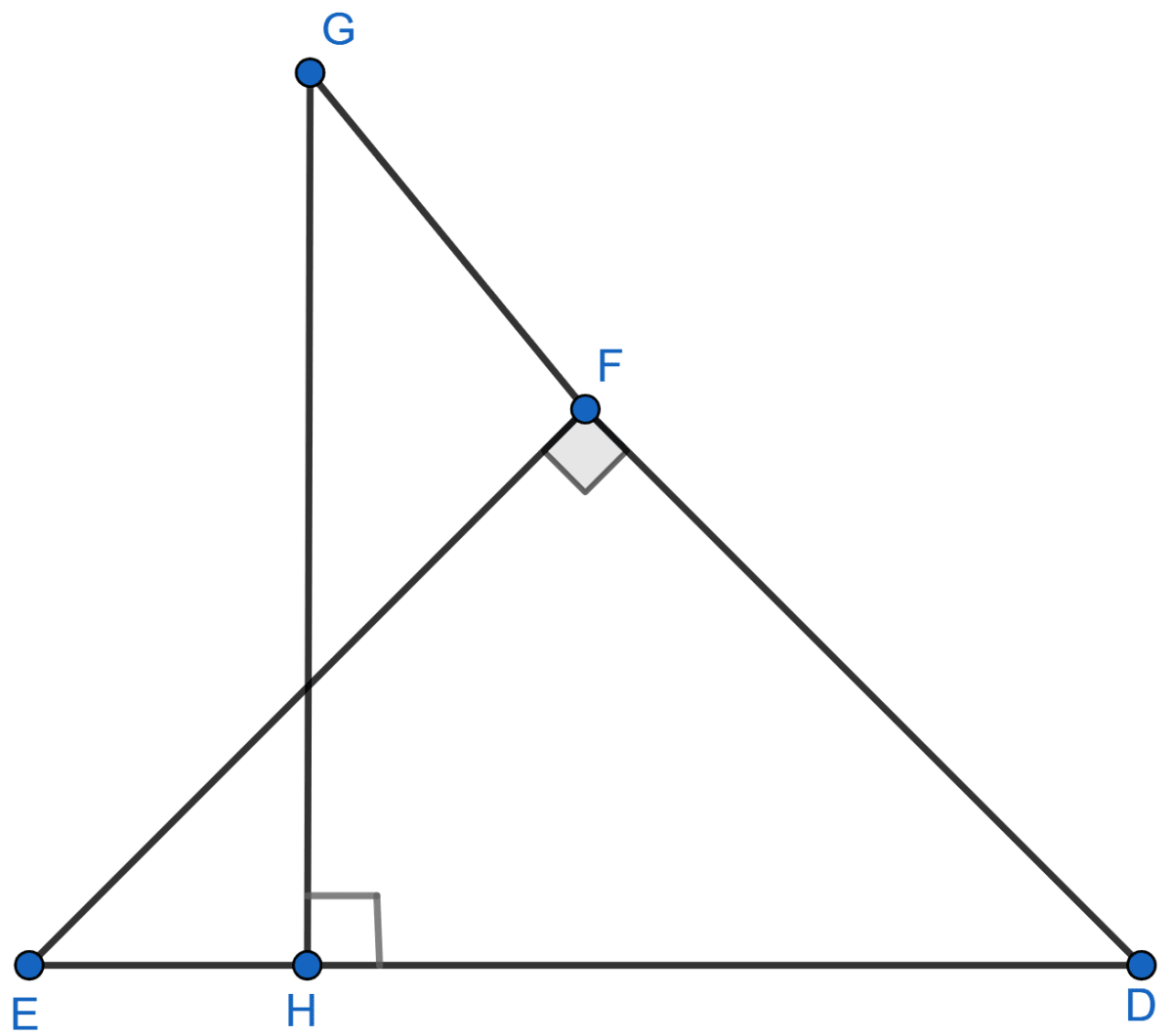
Given: ∠GHE = ∠DFE = 90°, DH = 8, DF = 12, DG = 3x – 1 and DE = 4x + 2.
Find: the lengths of segments DG and DE.
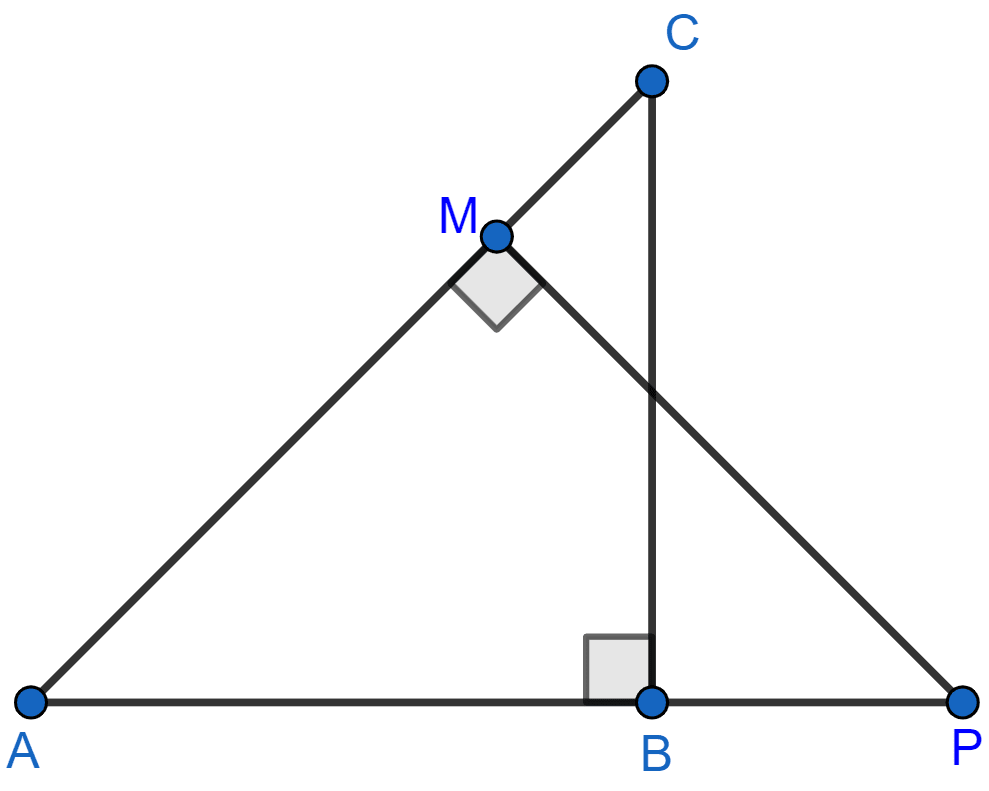
In the given figure, ΔABC and ΔAMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
(i) Prove that : ∆ABC ~ ∆AMP.
(ii) Find AB and BC.
In △PQR, ∠Q = 90° and QM is perpendicular to PR. Prove that :
(i) PQ2 = PM × PR
(ii) QR2 = PR × MR
(iii) PQ2 + QR2 = PR2