Mathematics
Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm and ∠ABC = 120°.
(i) Construct a circle circumscribing the triangle ABC.
(ii) Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Constructions
Answer
(i) Steps of construction :
Draw a line segment BC = 5.5 cm
From B draw a ray BX such that ∠XBC = 120°.
From B draw an arc of 6 cm cutting BX at A.
Join AC. ABC is the required triangle.
Construct perpendicular bisectors of AB and BC, such that they intersect at O.
With O as center and OA as radius draw a circle passing through A, B and C.
Hence, above is the required circumcircle of triangle ABC.
(ii) Steps of construction :
Draw perpendicular bisector of BC, such that it intersects the circle at D.
Join CD and AD. ABCD is the cyclic quadrilateral.
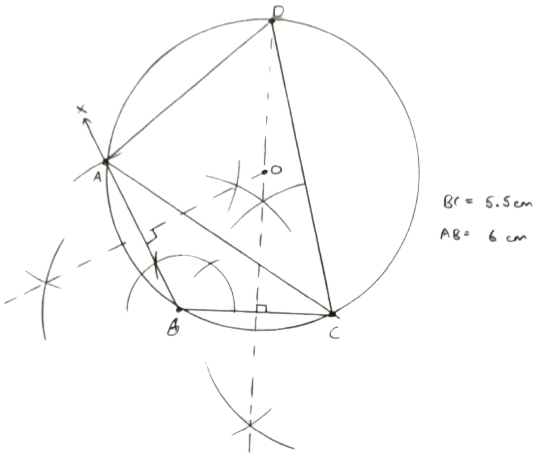
Hence, above is the required cyclic quadrilateral.
Answered By
Related Questions
Draw a circle circumscribing a regular hexagon with side = 5 cm.
Draw an inscribing circle of regular hexagon of side 5.8 cm.
Using a ruler and compasses only :
(i) Construct a triangle ABC with the following data :
AB = 3.5 cm, BC = 6 cm and ∠ABC = 120°.
(ii) In same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
(iii) Measure ∠BCP.
Draw a line AB = 5 cm. Mark a point C on AB such that AC = 3 cm. Using a ruler and a compass only, construct :
(i) a circle of radius 2.5 cm, passing through A and C.
(ii) construct two tangents to the circle from the external point B. Measure and record the length of the tangents.