Mathematics
By using ruler and compasses only, construct an isosceles triangle ABC in which BC = 5 cm, AB = AC and ∠BAC = 90°. Locate the point P such that
(i) P is equidistant from the sides BC and AC.
(ii) P is equidistant from the points B and C.
Answer
Steps of construction :
Make BC = 5 cm as base.
Create a semicircle with BC as diameter.
Make right bisector of BC and mark it as D.
Make angle bisector of ∠ACB. From graph, CE is the abgle bisector.
Mark point P where angle bisector ∠ACB i.e CE meets perpendicular bisector of BC i.e. AD.
Draw perpendicular from point P and it meets semicircle at point A.
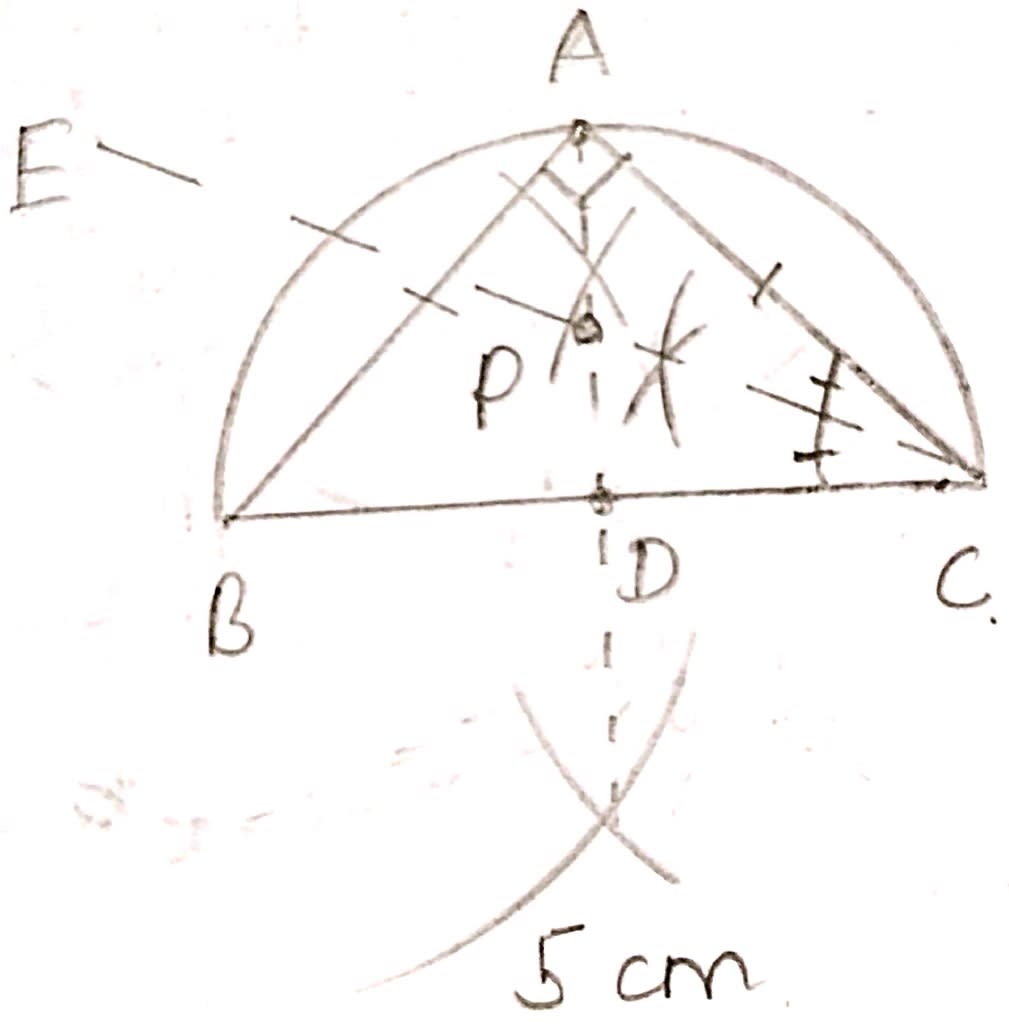
(i) We know that locus of points equidistant from two lines is the angle bisector of angle between them.
From figure,
CE is the angular bisector of ∠ACB, hence it will be equidistant from AC and BC.
(ii) We know that locus of points equidistant from two points is the perpendicular bisector of line segment joining them.
From figure,
AD is the perpendicular bisector of BC, hence it will be equidistant from B and C.
Both AD and CE meet at point P, so P is equidistant from BC and CA and also from B and C.
Related Questions
Using ruler and compasses only, construct a quadrilateral ABCD in which AB = 6 cm, BC = 5 cm, ∠B = 60°, AD = 5 cm and D is equidistant from AB and BC. Measure CD.
Without using set square or protractor, construct rhombus ABCD with sides of length 4 cm and diagonal AC of length 5 cm. Measure ∠ABC. Find the point R on AD such that RB = RC. Measure the length of AR.
Without using set square or protractor construct :
(i) Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.
(ii) Draw the locus of a point which moves so that it is always 2.5 cm from B.
(iii) Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.
(iv) Mark the point of intersection of the loci with the letter P and measure PC.
Using ruler and compass only, construct a semicircle with diameter BC = 7 cm. Locate a point P on the circumference of the semicircle such that A is equidistant from B and C. Completely the cyclic quadrilateral ABCD such that D is equidistant from AB and BC. Measure ∠ADC and write it down.