Mathematics
An open cylindrical vessel of internal diameter 7 cm and height 8 cm stands on a horizontal table. Inside this is placed a solid metallic right circular cone, the diameter of whose base is cm and height 8 cm. Find the volume of water required to fill the vessel.
If this cone is replaced by another cone, whose height is cm and the radius of whose base is 2 cm, find the drop in the water level.
Mensuration
Answer
Given,
Diameter of cylindrical vessel = 7 cm
Radius of cylindrical vessel (R) = = 3.5 cm
Height of cylindrical vessel (H) = 8 cm
Diameter of base of cone = cm
Radius of base of cone (r) = cm
Height of cone (h) = 8 cm
Volume of cylindrical vessel =
=
= 308 cm3.
Volume of original cone =
=
=
= cm3
Volume of water required to fill the vessel = Volume of cylindrical vessel - Volume of original cone
Given,
Radius of new cone (r1) = 2 cm
Height of new cone (h1) = cm
Volume of new cone = 1^2h1
Volume of water which comes down = Volume of original cone - Volume of new cone
=
= cm3.
Let drop in height of water be h2 cm.
Drop in volume of water = cm3
2 = \dfrac{55}{3} \\[1em] \Rightarrow \dfrac{22}{7} \times (3.5)^2 \times h2 = \dfrac{55}{3} \\[1em] \Rightarrow 22 \times 0.5 \times 3.5 \times h2 = \dfrac{55}{3} \\[1em] \Rightarrow 38.5 \times h2 = \dfrac{55}{3} \\[1em] \Rightarrow h2 = \dfrac{55}{115.5} \\[1em] \Rightarrow h2 = \dfrac{10}{21} \text{ cm}. \\[1em]
Hence, volume of water required to fill the vessel = 282.33 cm3 and drop in level of water = cm.
Answered By
Related Questions
Spherical marbles of diameter 1.4 cm are dropped into a beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm?
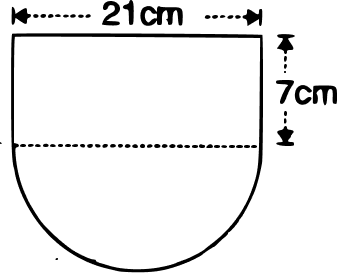
The given figure shows the cross-section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic meters correct to one place of decimal.
A cylindrical can, whose base is horizontal and of radius 3.5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate :
(i) the total surface area of the can in contact with water when the sphere is in it;
(ii) the depth of water in the can before the sphere was put into the can.
A hollow cylinder has solid hemisphere inward at one end and on the other end it is closed with a flat circular plate. The height of water is 10 cm when flat circular surface is downward. Find the level of water, when it is inverted upside down, common diameter is 7 cm and height of cylinder is 20 cm.