Mathematics
A cylindrical can, whose base is horizontal and of radius 3.5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate :
(i) the total surface area of the can in contact with water when the sphere is in it;
(ii) the depth of water in the can before the sphere was put into the can.
Mensuration
38 Likes
Answer
(i) Given,
Radius of base of cylindrical can (R) = 3.5 cm

Since,
When a sphere is placed in the can, the water just covers the sphere.
∴ Height (H) = 2R = 7 cm.
Total surface area = 2πRH + πR2
= πR(2H + R)
=
= 22 × 0.5 × (14 + 3.5)
= 192.5 cm2.
Hence, the total surface area of the can in contact with water when the sphere is in it = 192.5 cm2.
(ii) Let the depth of the water be h cm in the can.
Volume of water = Volume of cylinder - Volume of sphere
Hence, depth of water in the can before the sphere was put into the can = cm.
Answered By
23 Likes
Related Questions
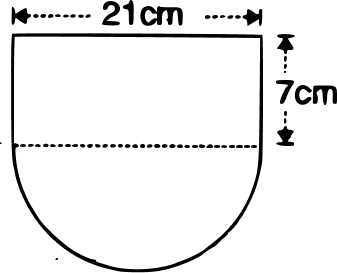
The given figure shows the cross-section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic meters correct to one place of decimal.
An open cylindrical vessel of internal diameter 7 cm and height 8 cm stands on a horizontal table. Inside this is placed a solid metallic right circular cone, the diameter of whose base is cm and height 8 cm. Find the volume of water required to fill the vessel.
If this cone is replaced by another cone, whose height is cm and the radius of whose base is 2 cm, find the drop in the water level.
A hollow cylinder has solid hemisphere inward at one end and on the other end it is closed with a flat circular plate. The height of water is 10 cm when flat circular surface is downward. Find the level of water, when it is inverted upside down, common diameter is 7 cm and height of cylinder is 20 cm.
The given figure shows a solid cylinder and a solid cone on it according to the given measurement, the total surface area of the solid in terms of π and r is :
4πr2
5πr2
6πr2
7πr2