An equilateral triangle of side 6 cm is inscribed in a circle. Find the radius of the circle.

From figure,

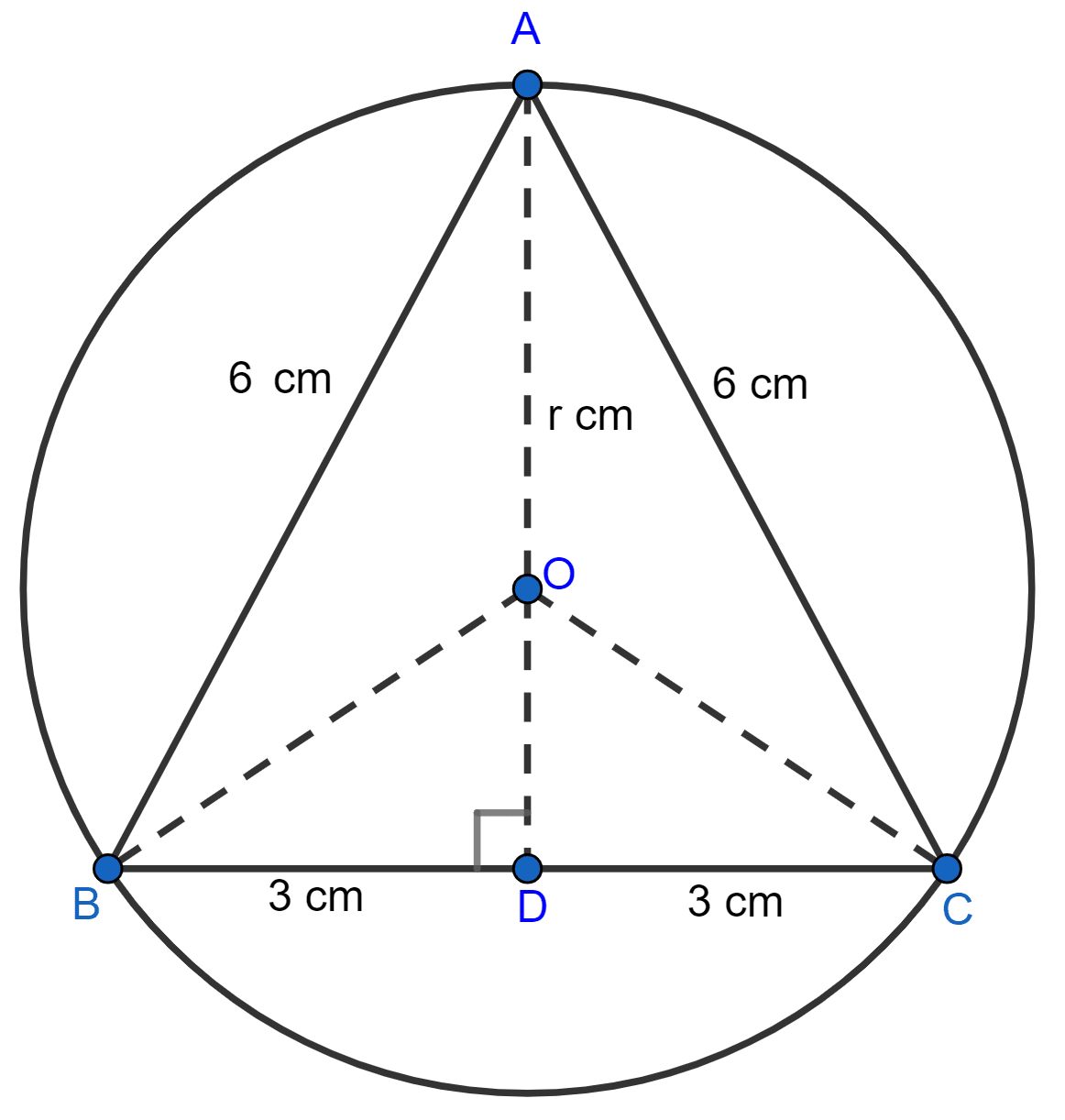
OA = radius = r cm.

BD = DC = $\dfrac{6}{2}$ = 3 cm (As perpendicular to a chord from the center of the circle bisects it)

In right angle triangle ABD,

⇒ AB² = AD² + BD²

⇒ 6² = AD² + 3²

⇒ AD² = 36 - 9

⇒ AD² = 27

⇒ AD = $\sqrt{27}$ = $3\sqrt{3}$ cm.

OD = AD - AO = $(3\sqrt{3} - r)$ cm.

In right angle triangle OBD,

⇒ OB = radius = r cm.

⇒ OB² = OD² + BD²

⇒ r² = $(3\sqrt{3} - r)$² + 3²

⇒ r² = 27 + r² - $6\sqrt{3}$r + 9

⇒ r² - r² + $6\sqrt{3}$r = 36

⇒ $6\sqrt{3}$r = 36

⇒ r = $\dfrac{36}{6\sqrt{3}} = 2\sqrt{3}$ cm.

Hence, radius = $2\sqrt{3}$ cm.